
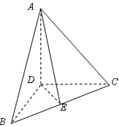
 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则$\overrightarrow{AE}•\overrightarrow{BC}$=0.
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则$\overrightarrow{AE}•\overrightarrow{BC}$=0. 分析 根据两个要求数量积的向量的位置,把这两个向量用以D为起点的向量来表示,整理出含有向量的数量积的表示形式,根据垂直和长度关系得到结果.
解答 解:∵$\overrightarrow{AE}•\overrightarrow{BC}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•($\overrightarrow{DC}-\overrightarrow{DB}$)
=$\frac{1}{2}$($\overrightarrow{DB}-\overrightarrow{DA}+\overrightarrow{DC}-\overrightarrow{DA}$)•($\overrightarrow{DC}$-$\overrightarrow{DB}$),
=$\frac{1}{2}$($\overrightarrow{DB}-2\overrightarrow{DA}+\overrightarrow{DC}$)•($\overrightarrow{DC}-\overrightarrow{DB}$),
=$\frac{1}{2}$$\overrightarrow{DB}•\overrightarrow{DC}$-$\frac{1}{2}$${\overrightarrow{DB}}^{2}$-$\overrightarrow{DA}•\overrightarrow{DC}$+$\overrightarrow{DA}•\overrightarrow{DB}$+$\frac{1}{2}$${\overrightarrow{DC}}^{2}$-$\frac{1}{2}$$\overrightarrow{DC}•\overrightarrow{DB}$,
∵DA,DB,DC两两垂直,且DB=DC,
∴$\overrightarrow{AE}•\overrightarrow{BC}$=0,
故答案为:0.
点评 本题考查空间向量的数量积的运算,本题解题的关键是把要求数量积的向量表示成已知向量的和或差的形式,再进行数量积的运算.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
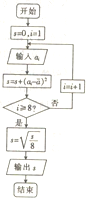 一天中对某人的心跳检测了8次,得到如表所示的数据
一天中对某人的心跳检测了8次,得到如表所示的数据| 检测次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 检测数据a(次/分钟) | 59 | 60 | 62 | 62 | 63 | 65 | 66 | 67 |
| A. | $\sqrt{7}$ | B. | 7 | C. | 8 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-e2+2e,0) | B. | (-e2+2e,+∞) | C. | (0,e2-2e) | D. | (-∞,-e2+2e) 第Ⅱ卷 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ③④ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com