
分析 (1)设C(x,y)(y≠0),得到G和AC中点的坐标,再由$\overrightarrow{GM}∥\overrightarrow{AB}$得到M的坐标,结合M是△ABC的外心,可得$\overrightarrow{MF}•\overrightarrow{AC}=0$,代入坐标整理得答案;
(2)假设存在满足条件的直线,并设其方程为y=kx+1,联立直线方程与E的方程,由∠PDQ为钝角,得$\overrightarrow{DP}•\overrightarrow{DQ}<0$,展开数量积,代入根与系数的关系,化为关于k的不等式得答案.
解答 解:(1)设C(x,y)(y≠0),则$G(\frac{x}{3},\frac{y}{3})$,
AC的中点$F(\frac{x-1}{2},\frac{y}{2})$,又$\overrightarrow{GM}∥\overrightarrow{AB}$,则$M(0,\frac{y}{3})$,
又M是△ABC的外心,
∴$\overrightarrow{MF}•\overrightarrow{AC}=0$,即$\frac{x-1}{2}•(x+1)+\frac{y}{6}•y=0$,
化简得,${x^2}+\frac{y^2}{3}=1(y≠0)$,
即点C的轨迹E的方程为${x^2}+\frac{y^2}{3}=1(y≠0)$;
(2)假设存在满足条件的直线,并设其方程为y=kx+1,
联立$\left\{\begin{array}{l}{x^2}+\frac{y^2}{3}=1\\ y=kx+1\end{array}\right.$,消去y得(k2+3)x2+2kx-2=0,
则△=12k2+24>0,
设P(x1,y1),Q(x2,y2),
则${x_1}+{x_2}=\frac{-2k}{{{k^3}+3}}$,${x_1}•{x_2}=\frac{-2}{{{k^3}+3}}$,
由∠PDQ为钝角,有$\overrightarrow{DP}•\overrightarrow{DQ}<0$,
即$({x_1}+\frac{1}{2})({x_2}+\frac{1}{2})+{y_1}{y_2}=({x_1}+\frac{1}{2})({x_2}+\frac{1}{2})+(k{x_1}+1)(k{x_2}+1)$
=$(1+{k^2}){x_1}{x_2}+(\frac{1}{2}+k)({x_1}+{x_2})+\frac{5}{4}<0$
整理得,11k2+4k-7>0,解得k<-1或$k>\frac{7}{11}$,
又当k=1时,直线过点A(-1,0),而A不在曲线E上,此时直线与曲线E只有一个交点,不符合题意,故舍去,
综上可知符合条件的直线存在,且其斜率的取值范围为k<-1或$\frac{7}{11}<k<1$或k>1.
点评 本题考查曲线方程的求法,考查了椭圆的简单性质,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a^{\frac{1}{3}}}$ | B. | ${a^{\frac{3}{2}}}$ | C. | ${a^{\frac{2}{3}}}$ | D. | ${a^{\frac{1}{6}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
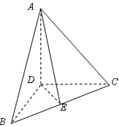 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则$\overrightarrow{AE}•\overrightarrow{BC}$=0.
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则$\overrightarrow{AE}•\overrightarrow{BC}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com