
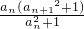 (n≥1,n∈N*).
(n≥1,n∈N*).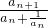 }是常数列;
}是常数列;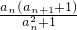 ,得
,得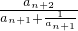 =
=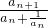 .
.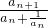 =
=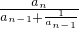 =
=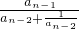 =…=
=…=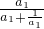 =
=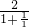 =1,
=1,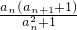 是常数列.(4分)
是常数列.(4分) .
.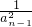 +2,
+2,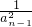 +2,
+2,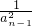 +2,
+2,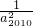 +…+
+…+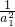 +2(2011-1)+1
+2(2011-1)+1 <4 022+
<4 022+ ×33
×33 ×33
×33 (19+4+10)<4 039<4 096=642.(14分)
(19+4+10)<4 039<4 096=642.(14分)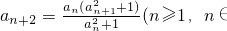 N*)变形化简得
N*)变形化简得 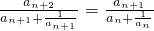 .将其迭代,利用a1=1,a2=2可以得到an+1与an之间的递推关系式;
.将其迭代,利用a1=1,a2=2可以得到an+1与an之间的递推关系式;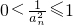 .又当n≥2时,
.又当n≥2时,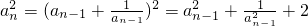 ,所以有
,所以有 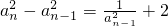 ,从而问题得证.
,从而问题得证.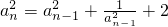 ,
,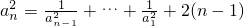 .
. 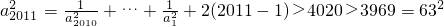
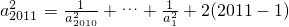 =
=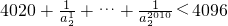 ,从而可解.
,从而可解.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
| a | 2 1 |
| a | 2 2 |
| a | 2 n |
| 2 |
| 1-3c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4x+m |
| 1 |
| 2 |
| 0 |
| n |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| an+1 | ||
(n+1
|
| an | ||
|
| 1 | ||
|
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com