
已知函数f(x)= ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
见解析
解析试题分析:本题是一个比较复杂的函数求零点的问题,通过转化为两个较熟悉的函数研究.容易得到两个数有三个交点,所以有三个零点.零点的范围不好确定,本题很巧妙地应用了零点定理,求出了个的范围.这种方法值得好好体会.
试题解析:由f(x)=0,得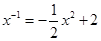 ,令
,令 ,
,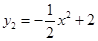 .分别画出它们的图象如图,其中抛物线的顶点坐标为(0,2),与x轴的交点为(-2,0)、(2,0),
.分别画出它们的图象如图,其中抛物线的顶点坐标为(0,2),与x轴的交点为(-2,0)、(2,0),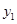 与
与 的图象有3个交点,从而函数f(x)有3个零点.由f(x)的解析式知x≠0,f(x)的图象在(-∞,0)和(0,+∞)上分别是连续不断地曲线,且
的图象有3个交点,从而函数f(x)有3个零点.由f(x)的解析式知x≠0,f(x)的图象在(-∞,0)和(0,+∞)上分别是连续不断地曲线,且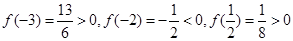
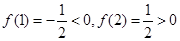 即
即 ,
,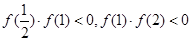 .所以三个零点分别在区间(-3,-2),
.所以三个零点分别在区间(-3,-2),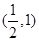 ,(1,2)内.
,(1,2)内.
考点:1.函数的零点转化为图解.2.零点定理.3.列举发现问题的思维.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
如图是某重点中学学校运动场平面图,运动场总面积15000平方米,运动场是由一个矩形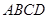 和分别以
和分别以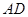 、
、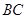 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,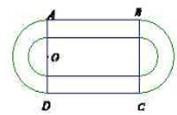
(Ⅰ)设半圆的半径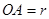 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积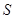 与
与 的函数关系式
的函数关系式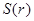 ;
;
(Ⅱ)由于受运动场两侧看台限制, 的范围为
的范围为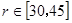 ,问当
,问当 为何值时,运动场造价最低(第2问
为何值时,运动场造价最低(第2问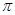 取3近似计算).
取3近似计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 ,且不等式
,且不等式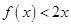 的解集为
的解集为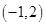 .
.
(1)方程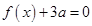 有两个相等的实根,求
有两个相等的实根,求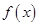 的解析式;
的解析式;
(2)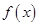 的最小值不大于
的最小值不大于 ,求实数
,求实数 的取值范围;
的取值范围;
(3) 如何取值时,函数
如何取值时,函数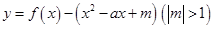 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com