设不等式
的解集为M，求当x∈M时函数
的最大、最小值.
科目：高中数学 来源： 题型：解答题
运货卡车以每小时
千米的速度匀速行驶130千米
（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油
升，司机的工资是每小时14元.
（1）求这次行车总费用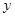
关于的表达式；
（2）当为何值时，这次行车的总费用最低，并求出最低费用的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某校课外兴趣小组的学生为了给学校边的一口被污染的池塘治污，他们通过实验后决定在池塘中投放一种能与水中的污染物质发生化学反应的药剂．已知每投放
个单位的药剂，它在水中释放的浓度
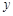（克/升）随着时间
（天）变化的函数关系式近似为
，其中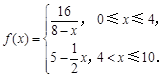
若多次投放，则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和．根据经验，当水中药剂的浓度不低于4（克/升）时，它才能起到有效治污的作用．
(Ⅰ)若一次投放4个单位的药剂，则有效治污时间可达几天？
(Ⅱ)若第一次投放2个单位的药剂，6天后再投放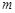
个单位的药剂，要使接下来的4天中能够持续有效治污，试求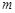的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在平面直角坐标系
中，已知椭圆
：
的离心率
，且椭圆C上一点
到点Q
的距离最大值为4，过点
的直线交椭圆于点
（Ⅰ）求椭圆C的方程；
（Ⅱ）设P为椭圆上一点，且满足
（O为坐标原点），当
时，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
图象上一点
处的切线方程为
.
（1）求
的值；
（2）若方程
在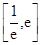
内有两个不等实根，求
的取值范围（其中
为自然对数的底数）；（3）令
，若
的图象与
轴交于
（其中
），
的中点为
，求证：在
处的导数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，最大值为8.
看成一个整体，由不等式
得出
，从而得到集合
；将
的二次函数，问题转化成二次函数在某个区间上的最值问题.
， 2分
， 5分
， 8分
，则
. 9分
在
时取最小值为
取，. 13分
，试利用基本初等函数的图象，判断f(x)有几个零点，并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1)．
上的单调函数
满足
，且对任意
都有
对任意
恒成立，求实数
的取值范围.
（其中
为常数且 
）的图象经过点
.
的解析式；
在
上恒成立，求实数
的取值范围.
．
时，求函数
的定义域；
的不等式
的解集是
，求
的取值范围．