
已知函数 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若方程 在
在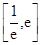 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(3)令
为自然对数的底数);(3)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 在
在 处的导数
处的导数
(1)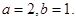 ;(2)
;(2)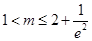 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)属于简单题,利用函数在 的导数值为斜率求解;(2)转化为函数
的导数值为斜率求解;(2)转化为函数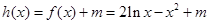 与
与 轴有2个交点,进来转化为求函数的最大值与最小值问题,利用导数判函数的单调性满足
轴有2个交点,进来转化为求函数的最大值与最小值问题,利用导数判函数的单调性满足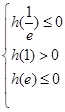 即可;(3)利用反证法求解,假设
即可;(3)利用反证法求解,假设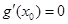 成立,由条件满足
成立,由条件满足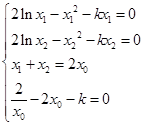 ,利用第1、2个条件求解
,利用第1、2个条件求解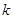 值,结合第4个条件得到
值,结合第4个条件得到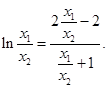 ,再利用函数的单调性充分证明假设错误,进而得证
,再利用函数的单调性充分证明假设错误,进而得证 在
在 处的导数
处的导数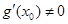 .
.
试题解析:(1)
 且
且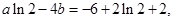
解得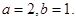 3分
3分
(2)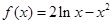 ,令
,令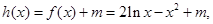
则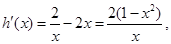
令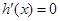 ,得
,得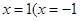 舍去).
舍去).
当 时,
时,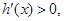
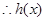 是增函数;
是增函数;
当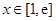 时,
时,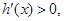
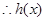 是减函数; 5分
是减函数; 5分
于是方程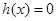 在
在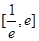 内有两个不等实根的充要条件是:
内有两个不等实根的充要条件是: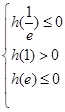 .
.
即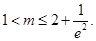 9分
9分
(3)由题意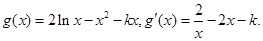
假设结论成立,则有: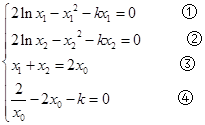 11分
11分
①-②,得
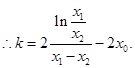
由④得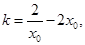
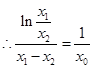
即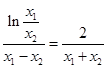 ,即
,即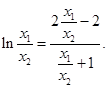 ⑤ 13分
⑤ 13分
令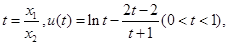
则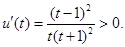
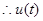 在(0,1)增函数,
在(0,1)增函数,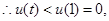
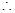 ⑤式不成立,与假设矛盾.
⑤式不成立,与假设矛盾.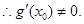 14分
14分
考点:1.利用导数判函数的单调性;2.函数的最值求解;3.反证法思想.


科目:高中数学 来源: 题型:解答题
如图,某生态园欲把一块四边形地 辟为水果园,其中
辟为水果园,其中 ,
, 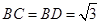 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 将四边形
将四边形 分成面积相等的两部分,设
分成面积相等的两部分,设 .
.
(1)求 的关系式;
的关系式;
(2)如果 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求 的长的最小值;
的长的最小值;
(3)如果 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么 的位置在哪里?
的位置在哪里?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数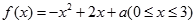 的最大值为
的最大值为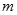 ,最小值为
,最小值为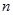 ,其中
,其中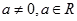 .
.
(1)求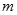 、
、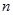 的值(用
的值(用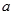 表示);
表示);
(2)已知角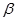 的顶点与平面直角坐标系
的顶点与平面直角坐标系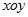 中的原点
中的原点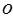 重合,始边与
重合,始边与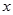 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点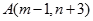 .求
.求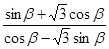 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度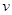 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度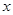 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当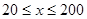 时,车流速度
时,车流速度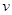 是车流密度
是车流密度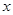 的一次函数.
的一次函数.
(Ⅰ)当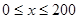 时,求函数
时,求函数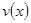 的表达式;
的表达式;
(Ⅱ)当车流密度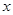 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)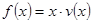 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com