
如图,某生态园欲把一块四边形地 辟为水果园,其中
辟为水果园,其中 ,
, 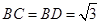 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 将四边形
将四边形 分成面积相等的两部分,设
分成面积相等的两部分,设 .
.
(1)求 的关系式;
的关系式;
(2)如果 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求 的长的最小值;
的长的最小值;
(3)如果 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么 的位置在哪里?
的位置在哪里?
(1)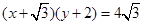 ;(2)
;(2)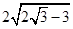 ;(3)P点在B处,Q点在E处.
;(3)P点在B处,Q点在E处.
解析试题分析:(1)由题目条件可求出 ,延长BD、CE交于点A,则由得出结论
,延长BD、CE交于点A,则由得出结论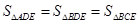 ,于是可知
,于是可知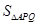 的面积,而它的面积又可用
的面积,而它的面积又可用 表示出来,于是问题得到解决;(2)
表示出来,于是问题得到解决;(2)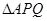 中利用余弦定理,可将
中利用余弦定理,可将 的长度用
的长度用 表示,再利用(1)的结果消去
表示,再利用(1)的结果消去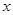 ,则得到
,则得到 关于
关于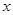 的函数关系式,然后利用基本不等式或求函数最值的一般方法求出函数的最小值或最大值,要注意函数的定义域;(3)思路同(2).
的函数关系式,然后利用基本不等式或求函数最值的一般方法求出函数的最小值或最大值,要注意函数的定义域;(3)思路同(2).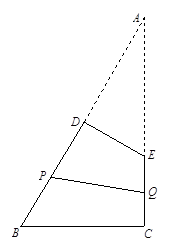
试题解析:(1)易知 ,延长BD、CE交于点A,则
,延长BD、CE交于点A,则 ,则
,则 .
.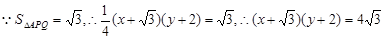 . 4分
. 4分
(2)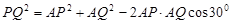
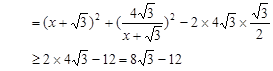 6分
6分
当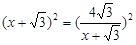 ,即
,即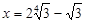 时,
时,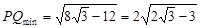 . 8分
. 8分
(3)令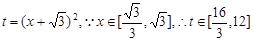 , 10分
, 10分
则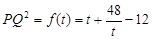 ,
,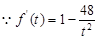 ,令
,令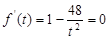 得,
得,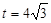 , 12分
, 12分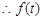 在
在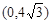 上是减函数,在
上是减函数,在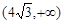 上是增函数,
上是增函数,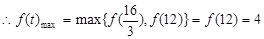 ,PQmax = 2, 14分
,PQmax = 2, 14分
此时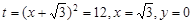 ,P点在B处,Q点在E处. 16分
,P点在B处,Q点在E处. 16分
考点:函数的应用、基本不等式、函数的最值.


科目:高中数学 来源: 题型:解答题
已知函数f(x)=a|x|+ (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=" f(" x),x∈[ 2,+∞), 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)从第几年开始,该机床开始盈利(盈利额为正值);
(Ⅲ)使用若干年后,对机床的处理方案有两种:
(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(2)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若方程 在
在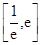 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(3)令
为自然对数的底数);(3)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 在
在 处的导数
处的导数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com