
设函数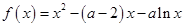 .
.
(1)求函数 的单调区间
的单调区间
(2)若函数 有两个零点
有两个零点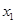 、
、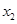 ,且
,且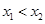 ,求证:
,求证: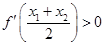 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)先求出函数 的定义域与导数
的定义域与导数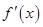 ,并对导数进行因式分解,然后对导数方程的根是否在定义域内进行分类讨论,从而确定函数
,并对导数进行因式分解,然后对导数方程的根是否在定义域内进行分类讨论,从而确定函数 相应的单调区间;(2)先利用函数
相应的单调区间;(2)先利用函数 有两个零点
有两个零点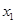 、
、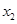 将
将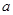 利用
利用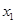 和
和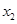 进行表示,于此同时,利用分析法将所要证明的问题进行转化,转化为
进行表示,于此同时,利用分析法将所要证明的问题进行转化,转化为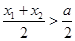 ,并结合前面
,并结合前面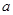 的结果,令
的结果,令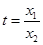 ,构造新函数利用导数来进行证明.
,构造新函数利用导数来进行证明.
试题解析:(1)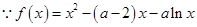 ,定义域为
,定义域为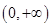 ,
, ,由于
,由于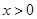 ,
, ,
,
①当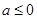 时,对任意
时,对任意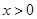 ,
, ,则函数
,则函数 的单调递增区间为
的单调递增区间为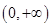 ;
;
②当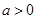 时,令
时,令 ,解得
,解得 ,
,
当 时,
时,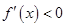 ,当
,当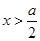 时,
时, ,
,
此时,函数 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
(2)因为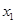 、
、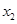 是函数
是函数 的两个零点,有
的两个零点,有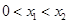 ,
,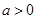
则 ,
, ,
,
两式相减得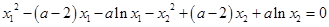 ,
,
即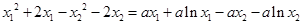

所以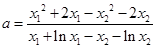
又因为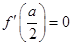 ,当
,当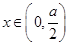 时,
时,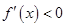 ;当
;当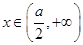 时,
时,
故只要证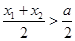 即可,即证明
即可,即证明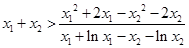 ,
,
即证明 ,
,
即证明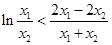 ,
,
设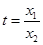
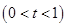 .令
.令 ,
,
则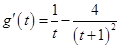
 ,因为
,因为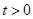 ,所以
,所以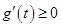 ,当且仅当
,当且仅当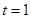 时,
时,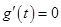
所以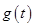 在
在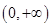 是增函数;又因为
是增函数;又因为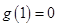 ,所以当
,所以当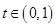 时,
时, 总成立.
总成立.
所以原题得证.
考点:1.分类讨论法;2.函数的单调区间;3.函数不等式


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
新晨投资公司拟投资开发某项新产品,市场评估能获得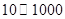 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
.
(1)设奖励方案的函数模型为 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 的基本要求.
的基本要求.
(2)下面是公司预设的两个奖励方案的函数模型:
① ; ②
; ②
试分别分析这两个函数模型是否符合公司要求.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某生态园欲把一块四边形地 辟为水果园,其中
辟为水果园,其中 ,
, 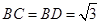 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 将四边形
将四边形 分成面积相等的两部分,设
分成面积相等的两部分,设 .
.
(1)求 的关系式;
的关系式;
(2)如果 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求 的长的最小值;
的长的最小值;
(3)如果 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么 的位置在哪里?
的位置在哪里?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系: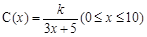 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定.大桥上的车距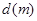 与车速
与车速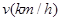 和车长
和车长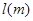 的关系满足:
的关系满足: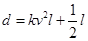 (
( 为正的常数),假定车身长为
为正的常数),假定车身长为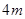 ,当车速为
,当车速为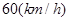 时,车距为2.66个车身长.
时,车距为2.66个车身长.
写出车距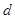 关于车速
关于车速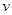 的函数关系式;
的函数关系式;
应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com