
新晨投资公司拟投资开发某项新产品,市场评估能获得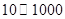 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
.
(1)设奖励方案的函数模型为 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 的基本要求.
的基本要求.
(2)下面是公司预设的两个奖励方案的函数模型:
① ; ②
; ②
试分别分析这两个函数模型是否符合公司要求.
(1)详见解析;(2)详见解析.
解析试题分析:(1)根据题中的条件对函数 的基本要求转化为数学语言;(2)对题中的两个函数是否满足(1)中的三个限制条件进行验证,对于函数上述两个函数是否满足题中的条件,主要是研究函数的单调性与最值以及恒成立问题,可以利用基本函数的单调性以及利用导数来进行求解.
的基本要求转化为数学语言;(2)对题中的两个函数是否满足(1)中的三个限制条件进行验证,对于函数上述两个函数是否满足题中的条件,主要是研究函数的单调性与最值以及恒成立问题,可以利用基本函数的单调性以及利用导数来进行求解.
试题解析:(1)由题意知,公司对奖励方案的函数模型 的基本要求是:
的基本要求是:
当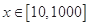 时,
时,
①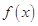 是增函数;②
是增函数;②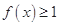 恒成立;③
恒成立;③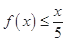 恒成立;
恒成立;
(2)①对于函数模型 :当
:当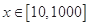 时,
时,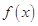 是增函数,
是增函数,
则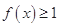 显然恒成立;
显然恒成立;
而若使函数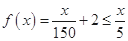 在
在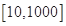 上恒成立,整理即
上恒成立,整理即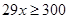 恒成立,而
恒成立,而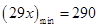 ,
,
∴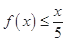 不恒成立.故该函数模型不符合公司要求.
不恒成立.故该函数模型不符合公司要求.
②对于函数模型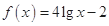 :
:
当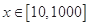 时,
时,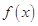 是增函数,则
是增函数,则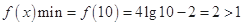 .∴
.∴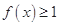 恒成立.
恒成立.
设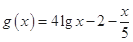 ,则
,则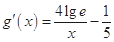 .
.
当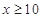 时,
时,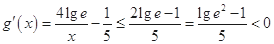 ,
,
所以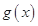 在
在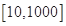 上是减函数,
上是减函数,
从而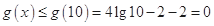 .
.
∴ ,即
,即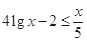 ,∴
,∴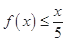 恒成立.
恒成立.
故该函数模型符合公司要求.
考点:1.函数的单调性;2.函数不等式


科目:高中数学 来源: 题型:解答题
某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为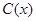 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,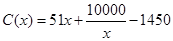 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数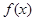 若存在
若存在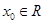 ,使得
,使得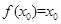 成立,则称
成立,则称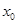 为
为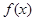 的不动点.
的不动点.
已知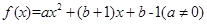
(1)当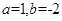 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数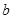 ,函数
,函数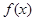 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(3)在(2)的条件下,若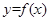 图象上
图象上 、
、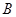 两点的横坐标是函数
两点的横坐标是函数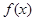 的不动点,且
的不动点,且 、
、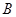 两点关于直线
两点关于直线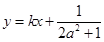 对称,求
对称,求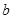 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=a|x|+ (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=" f(" x),x∈[ 2,+∞), 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
张林在李明的农场附近建了一个小型工厂,由于工厂生产须占用农场的部分资源,因此李明每年向张林索赔以弥补经济损失并获得一定净收入.工厂在不赔付农场的情况下,工厂的年利润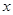 (元)与年产量
(元)与年产量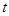 (吨)满足函数关系
(吨)满足函数关系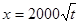 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场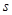 元(以下称
元(以下称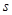 为赔付价格).
为赔付价格).
(Ⅰ)将工厂的年利润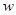 (元)表示为年产量
(元)表示为年产量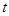 (吨)的函数,并求出工厂获得最大利润的年产量;
(吨)的函数,并求出工厂获得最大利润的年产量;
(Ⅱ)若农场每年受工厂生产影响的经济损失金额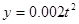 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格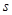 是多少?
是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com