
定义在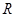 上的函数
上的函数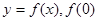
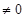 ,当
,当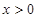 时,
时,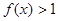 ,且对任意的
,且对任意的 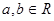 ,有
,有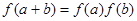 ,
,
(Ⅰ)求证: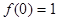 ;
;
(Ⅱ)求证:对任意的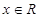 ,恒有
,恒有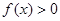 ;
;
(Ⅲ)若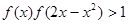 ,求
,求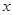 的取值范围.
的取值范围.
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)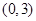 .
.
解析试题分析:(Ⅰ)令 即可得证;(Ⅱ)令
即可得证;(Ⅱ)令 得,
得, ,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明
,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明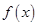 为增函数:任取x2>x1,则
为增函数:任取x2>x1,则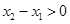 ,
,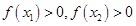 ,故
,故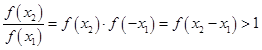 ,故其为增函数;然后利用单调性脱
,故其为增函数;然后利用单调性脱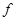 解一元二次不等式.
解一元二次不等式.
试题解析:(Ⅰ)令 ,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分
,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分
(Ⅱ)令 则 f(0)=f(x)f(-x)∴
则 f(0)=f(x)f(-x)∴ 4分
4分
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴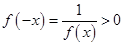 ,又x=0时,f(0)=1>0 6分
,又x=0时,f(0)=1>0 6分
∴对任意x∈R,f(x)>0 7分
(Ⅲ)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0 8分
∴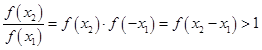
∴f(x2)>f(x1) ∴ f(x)在R上是增函数 10分
f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x)又1=f(0),f(x)在R上递增
∴由f(3x-x2)>f(0)得:x-x2>0 ∴ 0<x<3 13分
考点:抽象函数、增函数的证明、一元二次不等式解法.


科目:高中数学 来源: 题型:解答题
如图,某生态园欲把一块四边形地 辟为水果园,其中
辟为水果园,其中 ,
, 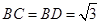 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 将四边形
将四边形 分成面积相等的两部分,设
分成面积相等的两部分,设 .
.
(1)求 的关系式;
的关系式;
(2)如果 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求 的长的最小值;
的长的最小值;
(3)如果 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么 的位置在哪里?
的位置在哪里?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数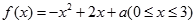 的最大值为
的最大值为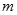 ,最小值为
,最小值为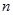 ,其中
,其中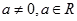 .
.
(1)求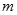 、
、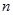 的值(用
的值(用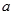 表示);
表示);
(2)已知角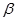 的顶点与平面直角坐标系
的顶点与平面直角坐标系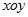 中的原点
中的原点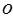 重合,始边与
重合,始边与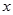 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点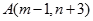 .求
.求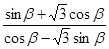 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
统计表明:某种型号的汽车在匀速行驶中每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大速度行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
国家助学贷款是由财政贴息的信用贷款(即无利息贷款),旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2013届毕业生小王在本科期间共申请了24000元助学贷款,并承诺在毕业后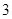 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第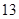 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多 元.
元.
(1)假设小王在第 个月还清贷款(
个月还清贷款( ),试用
),试用 和
和 表示小王第
表示小王第 (
( )个月的还款额
)个月的还款额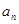 ;
;
(2)当 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款?
(3)在(2)的条件下,他还清最后一笔贷款的那个月工资的余额是否能满足此月 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: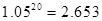 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com