
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ⊙
⊙ ![]() =mq-np,下面说法错误的是( )
=mq-np,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
【答案】B
【解析】解:对于A,若 ![]() 与
与 ![]() 共线,则有
共线,则有 ![]() ⊙
⊙ ![]() =mq-np=0,故A正确;
=mq-np=0,故A正确;
对于B,因为 ![]() ⊙
⊙ ![]() =pn-qm,而
=pn-qm,而 ![]() ⊙
⊙ ![]() =mq-np,所以有
=mq-np,所以有 ![]() ⊙
⊙ ![]()
![]()
![]() ⊙
⊙ ![]() ,故选项B错误,
,故选项B错误,
对于C, ![]() ⊙
⊙ ![]() =λqm﹣λpn,而
=λqm﹣λpn,而 ![]() ⊙
⊙ ![]() )=λ(qm﹣pn)=λqm﹣λpn,故C正确,
)=λ(qm﹣pn)=λqm﹣λpn,故C正确,
对于D,( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=|
)2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=| ![]() |2|
|2| ![]() |2 , D正确;
|2 , D正确;
故选B.
根据题意对选项逐一分析.若 ![]() 与
与 ![]() 共线,则有
共线,则有 ![]() ⊙
⊙ ![]() =mq-np=0,故A正确;
=mq-np=0,故A正确;
因为 ![]() ⊙
⊙ ![]() =pn-qm,而
=pn-qm,而 ![]() ⊙
⊙ ![]() =mq-np,所以有
=mq-np,所以有 ![]() ⊙
⊙ ![]()
![]()
![]() ⊙
⊙ ![]() ,故选项B错误,
,故选项B错误,
对于C, ![]() ⊙
⊙ ![]() =λqm﹣λpn,而
=λqm﹣λpn,而 ![]() ⊙
⊙ ![]() )=λ(qm﹣pn)=λqm﹣λpn,故C正确,
)=λ(qm﹣pn)=λqm﹣λpn,故C正确,
对于D,( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=|
)2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=| ![]() |2|
|2| ![]() |2 , D正确;
|2 , D正确;
得到答案.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如表数据:
单价x(元) | 18 | 19 | 20 | 21 | 22 |
销量y(册) | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和y对x的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年被业界称为![]() (虚拟现实技术)元年,未来
(虚拟现实技术)元年,未来![]() 技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某
技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某![]() 教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需
教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需![]() 团队投入15天时间,
团队投入15天时间, ![]() 团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需
团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需![]() 团队投入20天时间,
团队投入20天时间, ![]() 团队投入16天时间,总费用15万元,乙产品售价为25万元/件,
团队投入16天时间,总费用15万元,乙产品售价为25万元/件, ![]() 、
、![]() 两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 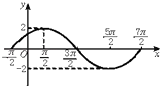
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() ,并且直线
,并且直线![]() 平分圆
平分圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在直线
两点,是否存在直线![]() ,使得
,使得![]() (
(![]() 为坐标原点),若存在,求出
为坐标原点),若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣lnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)﹣x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e为自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com