
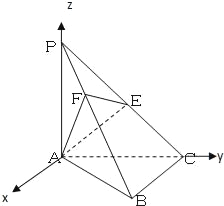
【题目】已知在三棱锥P﹣ABC中,PA⊥面ABC,AC⊥BC,且PA=AC=BC=1,点E是PC的中点,作EF⊥PB交PB于点F.
(Ⅰ)求证:PB⊥平面AEF;
(Ⅱ)求二面角A﹣PB﹣C的大小.

【答案】(Ⅰ)见解析;(2)60°.
【解析】试题分析:
(Ⅰ)要证直线PB与平面AEF垂直,就要证PB与平面AEF内两条相交直线垂直,其中已知有一个垂直:EF⊥PB,由等腰三角形性质知AE⊥PC,因此可先证AE⊥平面PBC得AE⊥PB,这又可通过证明BC⊥平面PAC得到;(Ⅱ)要求二面角大小,由图可建立空间直角坐标系(见解析),写出各点坐标,求出二面角两个面的法向量,由法向量夹角得二面角(相等或互补).
试题解析:
(Ⅰ)证明:∵PA⊥面ABC,BC面ABC,
∴PA⊥BC,又AC⊥BC,PA⊥BC,PA∩AC=A,∴BC⊥面PAC,
而AEPAC,∴BC⊥AE,又PA=AC,点E是PC的中点,∴AE⊥PC,
又AE⊥BC,BC∩PC=C,∴AE⊥面PBC,而PB面PBC,AE⊥PB,又EF⊥PB,AE⊥BP,AE∩EF=E,∴PB⊥平面AEF;
(Ⅱ)解:以A为坐标原点,AC所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,
∵PA=AC=BC=1,则A(0,0,0),P(0,0,1),C(0,1,0),B(1,1,0).
![]() .
.
设平面PAB的一个法向量为![]() ,
,
则由![]() ,得
,得![]() ,取y1=﹣1,得x1=1,z1=0,
,取y1=﹣1,得x1=1,z1=0,
∴![]() .
.
再设平面PBC的一个法向量为![]() ,
,
则由![]() ,得
,得![]() ,取z2=1,得y2=1,
,取z2=1,得y2=1,
∴![]() .
.
∴![]() .
.
∴二面角A﹣PB﹣C的大小为60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),它与曲线
(t为参数),它与曲线
C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(lga+2)x+lgb满足f(﹣1)=﹣2且对于任意x∈R,恒有f(x)≥2x成立.
(1)求实数a,b的值;
(2)解不等式f(x)<x+5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ),x∈R.
),x∈R.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)求函数f(x)在区间[-![]() ,
,![]() ]上的最小值和最大值,并求出取得最值时x的值.
]上的最小值和最大值,并求出取得最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),它与曲线
(t为参数),它与曲线
C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查甲、乙两种品牌商品的市场认可度,在某购物网点随机选取了14天,统计在某确定时间段的销量,得如下所示的统计图,根据统计图求:
(1)甲、乙两种品牌商品销量的中位数分别是多少?
(2)甲品牌商品销量在[20,50]间的频率是多少?
(3)甲、乙两个品牌商品哪个更受欢迎?并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点,F1(﹣c,0),F2(c,0),P为C1与C2在第一象限的交点,|PF1|=|F1F2|且|PF2|=5,若椭圆C1的离心率 ![]() ,则双曲线的离心率e2的范围是( )
,则双曲线的离心率e2的范围是( )
A.![]()
B.![]()
C.(2,3)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抛物线y=x2与直线y=2围成的封闭图形内任取一点A,O为坐标原点,则直线OA被该封闭图形解得的线段长小于 ![]() 的概率是( )
的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com