
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(1)证明:![]() ;
;
(2)若点![]() 为棱
为棱![]() 上一点,且
上一点,且![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
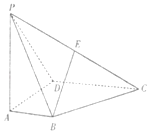
【答案】(1)证明见解析 (2)![]()
【解析】
(1)推导出![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能证明
轴,建立空间直角坐标系,利用向量法能证明![]() .
.
(2)求出![]() ,0,
,0,![]() 是平面
是平面![]() 的一个法向量,由
的一个法向量,由![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,求出
,求出![]() ,求出平面
,求出平面![]() 的法向量和平面
的法向量和平面![]() 法向量,利用向量法能求出二面角
法向量,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
解:(1)证明:![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() .
.
(2)解:由已知,设![]() ,
,![]() ,设
,设![]() ,
,
由(1)知,![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]() ,
,![]()
解得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() 平面
平面![]() ,
,![]()
![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() ,
,
解得![]() 或
或![]() (舍
(舍![]() ,
,![]()
![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则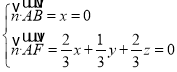 ,取
,取![]() ,得
,得![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,
,![]() ,
,![]()
设二面角![]() 的平面角为
的平面角为![]() ,
,
则二面角![]() 的余弦值为:
的余弦值为:![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() 为常数).
为常数).
(1)当![]() 时,讨论函数
时,讨论函数![]() 在
在![]() 的单调性;
的单调性;
(2)设![]() 可求导数,且它的导函数
可求导数,且它的导函数![]() 仍可求导数,则
仍可求导数,则![]() 再次求导所得函数称为原函数
再次求导所得函数称为原函数![]() 的二阶函数,记为
的二阶函数,记为![]() ,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间
,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间![]() 上是凸函数的充要条件是这个函数在
上是凸函数的充要条件是这个函数在![]() 的二阶导函数非负.
的二阶导函数非负.
若![]() 在
在![]() 不是凸函数,求
不是凸函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的10件产品中,有8件合格品、2件不合格品,合格品与不合格品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)2件都是合格品的概率;
(2)1件是合格品、1件是不合格品的概率;
(3)如果抽检的2件产品都是不合格品,那么这批产品将被退货,求这批产品被退货的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)
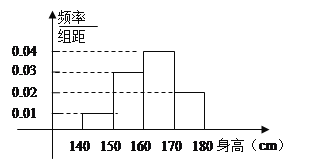
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
(2)在身高为140—160的学生中任选2个,求至少有一人的身高在150—160之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)=![]() x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
A. [-![]() ,
, ![]() ]
]
B. [-![]() ,
, ![]() ]
]
C. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
D. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为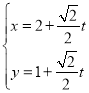 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆O:x2+y2=8内有一点P(﹣1,2),AB为过点P且倾斜角为α的弦,
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,写出直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com