
【题目】某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)
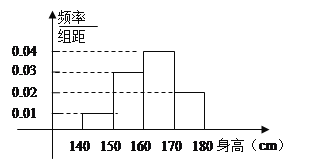
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
(2)在身高为140—160的学生中任选2个,求至少有一人的身高在150—160之间的概率.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)中位数的左边和右边的直方图的面积相等,由此可以估计中位数的值,平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和,由此可以估计平均数的值;(2)这![]() 名学生中,身高在
名学生中,身高在![]() 之间的有
之间的有![]() 个,身高在150—160之间的有
个,身高在150—160之间的有![]() 人,从中任选
人,从中任选![]() 人,共有
人,共有![]() 种不同的选法,而身高在
种不同的选法,而身高在![]() 之间的只有一种选法,从而至少有一人身高在150—160之间的有
之间的只有一种选法,从而至少有一人身高在150—160之间的有![]() 种,从而求出其概率.
种,从而求出其概率.
试题解析::(1)中位数的左边和右边的直方图的面积相等,由此可以估计中位数的值,
![]()
所以中位数的估计值为![]() .
.
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
则平均数的估计值为![]() .
.
(2)这![]() 名学生中,身高在
名学生中,身高在![]() 之间的有
之间的有![]() 个,分别为A,B,身高在150—160之间的有
个,分别为A,B,身高在150—160之间的有![]() 人,分别为C,D,E,F,G,H,
人,分别为C,D,E,F,G,H,
则从这![]() 人中任选
人中任选![]() 个的所有基本事件有AB,AC,AD,AE,AF,AG,AH,BC,BD,BE,BF,BG,BH,CD,CE,CF,CG,CH,
个的所有基本事件有AB,AC,AD,AE,AF,AG,AH,BC,BD,BE,BF,BG,BH,CD,CE,CF,CG,CH,
DE,DF,DG,DH,EF,EG,EH,FG,FH,GH共![]() 个,
个,
两个身高都在![]() 之间的事件有AB共
之间的事件有AB共![]() 个,
个,
所以至少有一个人在150—160之间的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】一般地,对于直线![]() 及直线
及直线![]() 外一点
外一点![]() ,我们有点
,我们有点![]() 到直线
到直线![]() 的距离公式为:
的距离公式为:![]() ”
”
(1)证明上述点![]() 到直线
到直线![]() 的距离公式
的距离公式
(2)设直线![]() ,试用上述公式求坐标原点
,试用上述公式求坐标原点![]() 到直线
到直线![]() 距离的最大值及取最大值时
距离的最大值及取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低汽车尾气的排放量,某厂生产甲乙两种不同型号的节排器,分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.
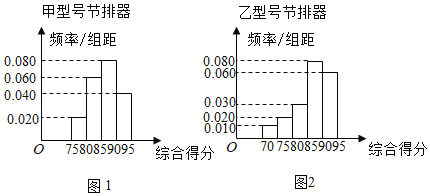
节排器等级及利润如表格表示,其中![]()
综合得分 | 节排器等级 | 节排器利润率 |
| 一级品 |
|
| 二级品 |
|
| 三级品 |
|
(1)若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件,再从这10件节排器中随机抽取3件,求至少有2件一级品的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求二级品数![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
②从长期来看,骰子哪种型号的节排器平均利润较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图,动直线![]() :
: ![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,
, ![]() 的半径为
的半径为![]() ,
, ![]() 是
是![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .求
.求![]() 的最大值,并求取得最大值时直线
的最大值,并求取得最大值时直线![]() 的斜率.
的斜率.
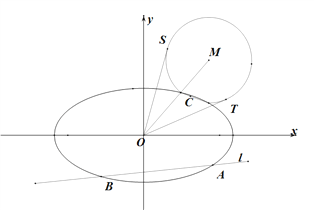
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com