
【题目】一般地,对于直线![]() 及直线
及直线![]() 外一点
外一点![]() ,我们有点
,我们有点![]() 到直线
到直线![]() 的距离公式为:
的距离公式为:![]() ”
”
(1)证明上述点![]() 到直线
到直线![]() 的距离公式
的距离公式
(2)设直线![]() ,试用上述公式求坐标原点
,试用上述公式求坐标原点![]() 到直线
到直线![]() 距离的最大值及取最大值时
距离的最大值及取最大值时![]() 的值.
的值.
【答案】(1)见解析 (2)![]()
【解析】
(1)设A≠0,B≠0,这时l与x轴、y轴都相交,过点P作x轴的平行线,交l于点R(x1,y0);作y轴的平行线,交l于点S(x0,y2),分别求出![]() .
. ![]() 、
、![]() 由三角形面积公式可知:d
由三角形面积公式可知:d![]() =
=![]()
![]() 即可得出.
即可得出.
(2)利用(1)中点到直线的距离公式,将题意转化为函数的单调性求最值.
解:(1)证明:设A≠0,B≠0,这时l与x轴、y轴都相交,过点P作x轴的平行线,交l于点R(x1,y0);作y轴的平行线,交l于点S(x0,y2),
由![]() 得
得![]() .
.
∴![]() =|x0﹣x1|=
=|x0﹣x1|=![]() ,
,
![]() =|y0﹣y2|=
=|y0﹣y2|=![]() ,
,
![]() =
=![]() |Ax0+By0+C|
|Ax0+By0+C|
由三角形面积公式可知:d![]() =
=![]()
![]()
∴![]()
可证明,当A=0时仍适用.
(2)由直线![]() ,由(1)中点到直线距离公式可得原点到直线
,由(1)中点到直线距离公式可得原点到直线![]() 距离为:
距离为:
![]() ,令/span>
,令/span>![]() ,则
,则![]() ,
,![]()
所以 ,
,![]()
当![]() 时,
时,![]()
当![]() 时,
时,
若![]() ,则
,则![]() 若
若![]() ,
,![]()
综上可知:![]() ,且当
,且当![]() ,即
,即![]() 时,可取最大值。
时,可取最大值。


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,若将f(x)图象上的所有点向右平移
)的部分图象如图所示,若将f(x)图象上的所有点向右平移 ![]() 个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( ) 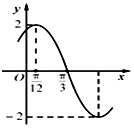
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
B.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
C.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
D.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程![]() 的曲线即为函数
的曲线即为函数![]() 的图像,对于函数
的图像,对于函数![]() ,有如下结论:①
,有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 不存在零点;③函数
不存在零点;③函数![]() 的值域是
的值域是![]() ;④
;④![]() 的图像不经过第一象限,其中正确结论的个数是___________
的图像不经过第一象限,其中正确结论的个数是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(2)当![]() 时,设
时,设![]() ,若给定
,若给定![]() ,对于两个大于1的正数
,对于两个大于1的正数![]() ,存在
,存在![]() 满足:
满足:![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)当![]() 时,设
时,设![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线l的极坐标方程为: ![]() ,曲线C的参数方程为:
,曲线C的参数方程为: ![]() (α为参数).
(α为参数).
(1)写出直线l的直角坐标方程;
(2)求曲线C上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:
车型 | A型 | B型 | C型 |
频数 | 20 | 40 | 40 |
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:
价格(万元) | 25 | 23.5 | 22 | 20.5 |
销售量(辆) | 30 | 33 | 36 | 39 |
已知A型汽车的购买量y与价格x符合如下线性回归方程: ![]() =
= ![]() x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2017年12月份人均用电情况进行统计后,按人均用电量分为
位居民2017年12月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是
五组,整理得到如下的频率分布直方图,则下列说法错误的是

A. ![]() 月份人均用电量人数最多的一组有
月份人均用电量人数最多的一组有![]() 人
人
B. ![]() 月份人均用电量不低于
月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. ![]() 月份人均用电量为
月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com