
���� �ٺ���y=$\frac{x-1}{x+1}$��ֻ�����ڣ�-�ޣ�-1���ͣ�-1��+�ޣ��ĵ����ԣ�
�ڢ۸��������κ�����ͼ��������жϣ�
���������C��f��x���ĵ�������C������б�ʣ�����ֱ��y=$\frac{1}{2}$x��ֱ���ɵ�m��ȡֵ��Χ��
��� �⣺���ڢٺ���y=$\frac{x-1}{x+1}$=1-$\frac{2}{x+1}$�����䣨-�ޣ�-1���ͣ�-1��+�ޣ����������������ڣ�-�ޣ�-1���ȣ�-1��+�ޣ��ϲ������������ʢٴ���
���ڢں���y=2sin��2x-$\frac{��}{4}$���ĵ���������-$\frac{��}{2}$+2k�С�2x-$\frac{��}{4}$��2k��+$\frac{��}{2}$����-$\frac{��}{8}$+k�С�x��k��+$\frac{3��}{8}$����k=0ʱ����Ϊ����-$\frac{��}{8}$��x��$\frac{3��}{8}$���ʢ���ȷ��
���ڢۺ���$f��x��=sin��2x+\frac{��}{3}��$ͼ��ĶԳ���Ϊ2x+$\frac{��}{3}$=k��+$\frac{��}{2}$����x=$\frac{k��}{2}$+$\frac{��}{12}$����k=1�գ�x=$\frac{7��}{12}$����k=0ʱ��x=$\frac{7��}{12}$���ʢ۴���
���ڢܡ�����C�ķ��̣�f��x��=ex-mx+1����f�䣨x��=ex-m��������C��������ֱ��y=$\frac{1}{2}$x��ֱ���ã�ex-m��•$\frac{1}{2}$=-1����m=ex+2��2���ʢ���ȷ��
�ʴ�Ϊ���ڢܣ�
���� ����ͨ��������ٵ��ж��������˺����ĵ����ԣ����Ǻ��������ʣ�����֪ʶ��Ӧ�ã������׳�������Ŀ�������е��⣮


 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Բ | B�� | ������ | C�� | ��Բ | D�� | ˫���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{5}{2}\sqrt{21}$ | B�� | $\frac{25}{4}$ | C�� | $\frac{15}{4}$ | D�� | $\frac{3}{2}\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
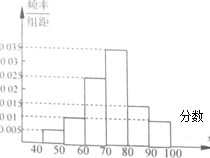 ��100��ѧ����ѧϰ�ɼ�����ͳ�ƣ��õ�����Ƶ��ֱ��ͼ��ͼ��ʾ���ֹ涨������70��Ϊ�ϸ���ϸ��������60��
��100��ѧ����ѧϰ�ɼ�����ͳ�ƣ��õ�����Ƶ��ֱ��ͼ��ͼ��ʾ���ֹ涨������70��Ϊ�ϸ���ϸ��������60���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{25}$ | B�� | $-\frac{7}{25}$ | C�� | $\frac{24}{25}$ | D�� | $-\frac{24}{25}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��0��\frac{1}{4}��$ | B�� | $��0��\frac{{\sqrt{3}}}{2}��$ | C�� | $��0��\frac{1}{2}��$ | D�� | ��$\frac{1}{4}$��$\frac{\sqrt{3}}{2}$�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com