
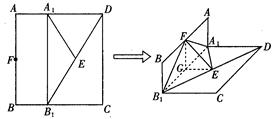
如图,已知长方形ABCD中,AB=2,A1,B1分别是AD,BC边上的点,且AA1=BB1="1," E,F分别为B1D与AB的中点. 把长方形ABCD沿直线 折成直角二面角,且
折成直角二面角,且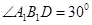 .
.
(1)求证: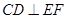
(2)求三棱锥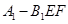 的体积.
的体积.
(1)根据题意,由于AA1⊥A1B1,同时FG//AA1,故FG⊥A1B1 ,那么结合A1B1⊥面EFG,可得A1B1⊥EF
得到结论。
(2)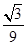
解析试题分析:解:(I)证明:因为AA1=BB1="1," 且AA1//BB1,所以四边形ABB1A1为矩形,故AA1⊥A1B1,
取A1B1的中点G,边接EG,FG,因为F为AB的中点,所以AF//A1G,且AF=A1G,可得四边形AFGA1是平行四边形,所以FG//AA1,故FG⊥A1B1 ,同理可得EG⊥A1B1,所以A1B1⊥面EFG,可得A1B1⊥EF. 因为CD//A1B1,所以CD⊥EF. (6分)
(II)因为∠A1B1D=30°,所以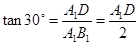 ,
,
可得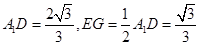 ,因为二面角A-A1B1-D为直二面角,由(I)可知FG⊥面A1B1E, 所以
,因为二面角A-A1B1-D为直二面角,由(I)可知FG⊥面A1B1E, 所以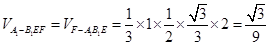 (12分)
(12分)
考点:三棱锥的体积以及线线垂直
点评:主要是考查了线线垂直以及三棱锥体积的运用,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证: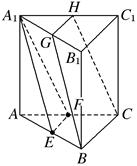
(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在长方体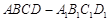 中,
中,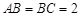 ,过
,过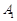 、
、 、
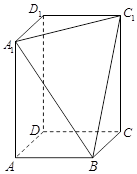
、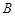 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体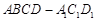 ,且这个几何体的体积为
,且这个几何体的体积为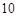 .
.
(1)求棱 的长;
的长;
(2)若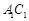 的中点为
的中点为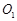 ,求异面直线
,求异面直线 与
与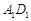 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱(侧棱垂直底面)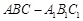 中,M、N分别是BC、AC1中点,AA1=2,AB=
中,M、N分别是BC、AC1中点,AA1=2,AB=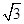 ,AC=AM=1.
,AC=AM=1.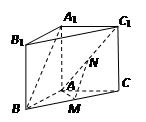
(1)证明:MN∥平面A1ABB1;
(2)求几何体C—MNA的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com