Question

4．求下列函数的值域．
（1）y=$\sqrt{x}$+1；
（2）y=2x+4$\sqrt{1-x}$；
（3）y=$\frac{2x}{3x-4}$；
（4）y=$\frac{x^2+4x-5}{x^2-3x+2}$；
（5）y=$\frac{x^2+4x-5}{x^2-x+2}$；
（6）y=$\left\{\begin{array}{l}{\frac{1}{x}，0＜x＜1}\\{x，x≥1}\end{array}\right.$；
（7）y=|x+1|+|x-2|．

Answer 1

分析 （1）直接由函数的单调性求函数的值域；
（2）利用换元法求函数的值域；
（3）把函数解析式变形，借助于反比例函数的值域求得答案；
（4）（5）利用判别式法求函数的值域；
（6）由题意画出图形，数形结合得答案；
（7）由绝对值的几何意义求得函数值域．

解答 解：（1）函数y=$\sqrt{x}$+1的定义域为[0，+∞），又函数为增函数，∴其值域为[1，+∞）；
（2）令$\sqrt{1-x}=t（t≥0）$，则x=1-t²，∴y=2x+4$\sqrt{1-x}$可化为g（t）=-2t²+4t+2=-2（t-1）²+4≤4，
∴函数y=2x+4$\sqrt{1-x}$的值域为（-∞，4]；
（3）由y=$\frac{2x}{3x-4}$=$\frac{\frac{2}{3}（3x-4）+\frac{8}{3}}{3x-4}=\frac{8}{3（3x-4）}+\frac{2}{3}$，
∵$\frac{8}{3（3x-4）}≠0$，∴y$≠\frac{2}{3}$，即y=$\frac{2x}{3x-4}$的值域为（$-∞，\frac{2}{3}$）∪（$\frac{2}{3}，+∞$）；
（4）由y=$\frac{x^2+4x-5}{x^2-3x+2}$，得（y-1）x²-（3y+4）x+2y+5=0．
当y=1时，方程化为7x=7，x=1；
当y≠1时，由△=[-（3y+4）]²-4（y-1）（2y+5）≥0，得（y+6）²≥0，∴y≠1．
综上，函数y=$\frac{x^2+4x-5}{x^2-3x+2}$的值域为R；
（5）由y=$\frac{x^2+4x-5}{x^2-x+2}$，得（y-1）x²-（y+4）x+2y+5=0．
当y=1时，方程化为5x=7，即x=$\frac{7}{5}$；
当y≠1时，由△=（y+4）²-4（y-1）（2y+5）≥0，解得：$-\frac{18}{7}≤y≤2$且y≠1．
综上，函数y=$\left\{\begin{array}{l}{\frac{1}{x}，0＜x＜1}\\{x，x≥1}\end{array}\right.$的值域为[$-\frac{18}{7}，2$]；
（6）函数y=$\left\{\begin{array}{l}{\frac{1}{x}，0＜x＜1}\\{x，x≥1}\end{array}\right.$的图象如图：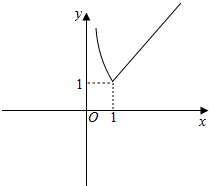

∴函数y=$\left\{\begin{array}{l}{\frac{1}{x}，0＜x＜1}\\{x，x≥1}\end{array}\right.$的值域为[1，+∞）；
（7）由绝对值的几何意义可知，y=|x+1|+|x-2|为数轴上的动点x到两定点-1、2的距离和，
∴函数y=|x+1|+|x-2|的最小值为3，即y=|x+1|+|x-2|的值域为[3，+∞）．

点评 本题考查函数的值域及其求法，训练了利用换元法和判别式法求函数的值域，是中档题．