
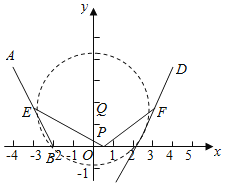
【题目】如图,在折线![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,若折线上满足条件
的中点,若折线上满足条件![]() 的点
的点![]() 至少有
至少有![]() 个,则实数
个,则实数![]() 的取值范围是___________.
的取值范围是___________.

【答案】![]()
【解析】
以BC的垂直平分线为y轴,以BC为x轴,建立如图所示的平面直角坐标系,分别表示各个点的坐标,设P(x,y),根据向量的数量积可得当k+9>0时,点P的轨迹为以(0,![]() )为圆心,以
)为圆心,以![]() 为半径的圆,结合图象,即可求出满足条件
为半径的圆,结合图象,即可求出满足条件![]() 的点P至少有4个的k的取值范围.
的点P至少有4个的k的取值范围.
解:以BC的垂直平分线为y轴,以BC为x轴,建立如图所示的平面直角坐标系,
∵AB=BC=CD=4,∠ABC=∠BCD=120°,
∴B(﹣2.0),C(2,0),A(﹣4,2![]() ),D(4,2
),D(4,2![]() ),
),
∵E、F分别是AB、CD的中点,
∴E(﹣3,![]() ),F(3,
),F(3,![]() ),
),
设P(x,y),﹣4≤x≤4,0≤y≤2![]() ,
,
∵![]() ,
,
∴(﹣3﹣x,![]() (3﹣x,
(3﹣x,![]() y)=
y)=![]() ,
,
即![]() ,
,
当k+9>0时,点P的轨迹为以(0,![]() )为圆心,以
)为圆心,以![]() 为半径的圆,
为半径的圆,
当圆与直线DC相切时,此时圆的半径r![]() ,此时点有2个,
,此时点有2个,
当圆经过点C时,此时圆的半径为r![]() ,此时点P有4个,
,此时点P有4个,
∵满足条件![]() 的点P至少有4个,结合图象可得,
的点P至少有4个,结合图象可得,
∴![]() k+9≤7,
k+9≤7,
解得![]() k≤﹣2,
k≤﹣2,
故实数k的取值范围为[![]() ,﹣2],
,﹣2],
故答案为:[![]() ,﹣2]
,﹣2]


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】春节来临之际,某超市为了确定此次春节年货的进货方案,统计去年春节前后50天年货的日销售量(单位:kg),得到如图所示的频率分布直方图.
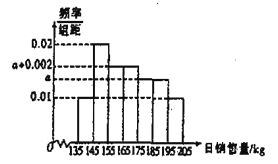
(1)求这50天超市日销售量![]() 的平均数;(视频率为概率,以各组区间的中点值代表该组的值)
的平均数;(视频率为概率,以各组区间的中点值代表该组的值)
(2)先从日销售在![]() ,
,![]() ,
,![]() 内的天数中,按分层抽样随机抽取4天进行比较研究,再从中选2天,求这2天的日销售量都在
内的天数中,按分层抽样随机抽取4天进行比较研究,再从中选2天,求这2天的日销售量都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足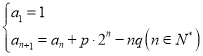 ,其中
,其中![]() .
.
(1)若数列前四项![]() ,
,![]() ,
,![]() ,
,![]() 依次成等差数列,求
依次成等差数列,求![]() ,
,![]() 的值;
的值;
(2)若![]() ,且数列
,且数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 是数列
是数列![]() 的最小项,求
的最小项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华东师大二附中乐东黄流中学位于我国南海边,有一片美丽的沙滩和一弯天然的海滨浴场.如图,海岸线MAN,![]() ,
,![]() (海岸线MAN上方是大海),现用长为BC的栏网围成一个三角形学生游泳场所,其中
(海岸线MAN上方是大海),现用长为BC的栏网围成一个三角形学生游泳场所,其中![]() .
.
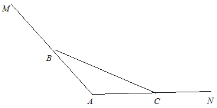
(1)若![]() ,求三角形游泳场所面积最大值;
,求三角形游泳场所面积最大值;
(2)若BC=600,![]() ,由于学生人数的增加需要扩大游泳场所面积,现在折线MBCN上方选点D,现用长为BD,DC的栏围成一个四边形游泳场所DBAC,使
,由于学生人数的增加需要扩大游泳场所面积,现在折线MBCN上方选点D,现用长为BD,DC的栏围成一个四边形游泳场所DBAC,使![]() ,求四边形游泳场所DBAC的最大面积.
,求四边形游泳场所DBAC的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=
=1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=![]() ,△BF1F2为直角三角形.
,△BF1F2为直角三角形.
(1)求椭圆C的方程;
(2)设直线y=kx+2与椭圆交于P、Q两点,且OP⊥OQ,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解贵州省某州2020届高三理科生的化学成绩的情况,该州教育局组织高三理科生进行了摸底考试,现从参加考试的学生中随机抽取了100名理科生,,将他们的化学成绩(满分为100分)分为![]()
![]()
![]()
![]()
![]()
![]() 6组,得到如图所示的频率分布直方图.
6组,得到如图所示的频率分布直方图.

(1)求a的值;
(2)记A表示事件“从参加考试的所有理科生中随机抽取一名学生,该学生的化学成绩不低于70分”,试估计事件A发生的概率;
(3)在抽取的100名理科生中,采用分层抽样的方法从成绩在![]() 内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在
内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在![]() 内的人数为X,求X的分布列与数学期望.
内的人数为X,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com