
【题目】已知数列![]() 满足
满足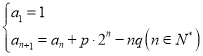 ,其中
,其中![]() .
.
(1)若数列前四项![]() ,
,![]() ,
,![]() ,
,![]() 依次成等差数列,求
依次成等差数列,求![]() ,
,![]() 的值;
的值;
(2)若![]() ,且数列
,且数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 是数列
是数列![]() 的最小项,求
的最小项,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)答案不唯一,见解析 (3)
(2)答案不唯一,见解析 (3)![]()
【解析】
(1)由已知求出![]() ,由等差数列的定义得
,由等差数列的定义得![]() 的方程可求解;
的方程可求解;
(2)由![]() 求出
求出![]() 值,代入已知递推式求出
值,代入已知递推式求出![]() ,验证它是等比数列;
,验证它是等比数列;
(3)当![]() 时,用累加法求得
时,用累加法求得![]() ,由
,由![]() 恒成立得,
恒成立得,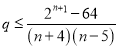 恒成立.用作差法证明数列
恒成立.用作差法证明数列![]() 是递增数列,从而可得最小值,得
是递增数列,从而可得最小值,得![]() 的一个范围,再由
的一个范围,再由![]() 得
得![]() 的另外一些范围后可得
的另外一些范围后可得![]() 的范围
的范围
(1)由已知递推式可得,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() .
.
由等差数列知,![]() ,得
,得![]() ;
;
(2)![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,
,![]() ,满足题意;
,满足题意;
当![]() 时,由累加法得
时,由累加法得![]() ,满足题意;
,满足题意;
(3)![]() 时,
时,
![]() ,
,
![]()
![]() ,
,
当![]() 时,由
时,由![]() 恒成立得,
恒成立得,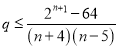 恒成立.
恒成立.
设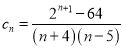 ,只需求出
,只需求出![]() 的最小值.
的最小值.
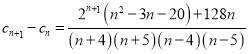 .
.
当![]() 时,
时,![]() ,有
,有![]() ;
;
当![]() 时,直接验证
时,直接验证![]() ;
;
故![]() 为最小值,其值为
为最小值,其值为![]() ,∴
,∴![]() ;
;
当![]() 时,需满足
时,需满足![]() 恒成立,
恒成立,
对![]() 验证,
验证,
![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() .
.
综上,![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】某电器专卖店销售某种型号的空调,记第![]() 天(
天(![]() ,
,![]() )的日销售量为
)的日销售量为![]() (单位;台).函数
(单位;台).函数![]() 图象中的点分别在两条直线上,如图,该两直线交点的横坐标为
图象中的点分别在两条直线上,如图,该两直线交点的横坐标为![]() ,已知
,已知![]() 时,函数
时,函数![]() .
.

(1)当![]() 时,求函数
时,求函数![]() 的解析式;
的解析式;
(2)求![]() 的值及该店前
的值及该店前![]() 天此型号空调的销售总量;
天此型号空调的销售总量;
(3)按照经验判断,当该店此型号空调的销售总量达到或超过![]() 台,且日销售量仍持续增加时,该型号空调开始旺销,问该店此型号空调销售到第几天时,才可被认为开始旺销?
台,且日销售量仍持续增加时,该型号空调开始旺销,问该店此型号空调销售到第几天时,才可被认为开始旺销?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某传动装置由两个陀螺![]() ,
,![]() 组成,陀螺之间没有滑动,每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的
组成,陀螺之间没有滑动,每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的![]() ,且
,且![]() ,
,![]() 的轴相互垂直,它们相接触的直线与
的轴相互垂直,它们相接触的直线与![]() 的轴所成角
的轴所成角![]() ,若陀螺
,若陀螺![]() 中圆锥的底面半径为
中圆锥的底面半径为![]() (
(![]() );
);
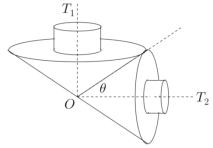
(1)求陀螺![]() 的体积;
的体积;
(2)当陀螺![]() 转动一圈时,陀螺
转动一圈时,陀螺![]() 中圆锥底面圆周上一点
中圆锥底面圆周上一点![]() 转动到点
转动到点![]() ,求
,求![]() 与
与![]() 之间的距离;
之间的距离;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函数
),都在函数![]() (
(![]() ,
,![]() )的图像上;
)的图像上;
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等比数列;
是等比数列;
(2)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,若函数
,若函数![]() 与函数
与函数![]() 的图像有公共点
的图像有公共点![]() ,求证:
,求证:![]() 在直线
在直线![]() 上;
上;
(3)设![]() ,
,![]() (
(![]() ),过点
),过点![]() 、
、![]() 的直线
的直线![]() 与两坐标轴围成的三角形面积为
与两坐标轴围成的三角形面积为![]() ,问:数列
,问:数列![]() 是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
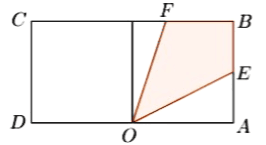
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(3)若探照灯每9分钟旋转“一个来回”(![]() 自
自![]() 转到
转到![]() ,再回到
,再回到![]() ,称“一个来回”,忽略
,称“一个来回”,忽略![]() 在
在![]() 及
及![]() 处所用的时间),且转动的角速度大小一定,设
处所用的时间),且转动的角速度大小一定,设![]() 边上有一点
边上有一点![]() ,且
,且![]() ,求点
,求点![]() 在“一个来回”中被照到的时间.
在“一个来回”中被照到的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
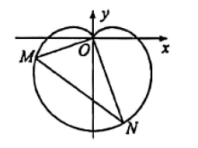
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com