【题目】如图，已知P（x0 ， y0）是椭圆C： 
=1上一点，过原点的斜率分别为k1 ， k2的两条直线与圆（x﹣x0）2+（y﹣y0）2= 
均相切，且交椭圆于A，B两点．
（1）求证：k1k2=﹣ 
；
（2）求|OA||OB|得最大值．
【答案】
（1）
证明：由圆P与直线OA：y=k1x相切，
可得 
= 
，
即（4﹣5x02）k12+10x0y0k1+4﹣5y02=0，
同理，（4﹣5x02）k22+10x0y0k2+4﹣5y02=0，
即有k1，k2是方程（4﹣5x02）k2+10x0y0k+4﹣5y02=0的两根，
可得k1k2= 
= 
=﹣ 
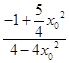（2）
解：设A（x1，y1），B（x2，y2），联立 
，
解得x12= 
，y12= 
，
同理，x22= 
，y22= 
，
（|OA||OB|）2=（ + ）（ + ），
∴|OA||OB|=2 
=2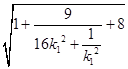 
≤ 
当且仅当k1=± 
时，取等号，
可得|OA||OB|的最大值为
【解析】（1）推导出k1 ， k2是方程（4﹣5x02）k2+10x0y0k+4﹣5y02=0的两根，由此能利用韦达定理能求出k1k2为定值；（2）设A（x1 ， y1），B（x2 ， y2），联立 ，由此利用椭圆性质，结合已知条件运用基本不等式能求出|OA||OB|的最大值．
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案，需要熟知椭圆标准方程焦点在x轴：
，焦点在y轴：
．
科目：高中数学 来源： 题型：
【题目】某经销商计划销售一款新型的空气净化器，经市场调研发现以下规律：当每台净化器的利润为 x （单位：元， x 0 ）时，销售量 q(x) （单位：百台）与 x 的关系满足：若 x 不超过 20 ， 则 
；若 x 大于或等于180 ，则销售量为零；当 20 ≤ x ≤180 时，
（ a ， b 为实常数）．
（Ⅰ）求函数 q(x) 的表达式；
（Ⅱ）当 x 为多少时，总利润（单位：元）取得最大值，并求出该最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3，从盒中任取3张卡片.
（1）求所取3张卡片上的数字完全相同的概率;
（2）
表示所取3张卡片上的数字的中位数，求的分布列与数学期望.
（注：若三个数
满足
，则称
为这三个数的中位数）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|xex+1|，关于x的方程f2（x）+2sinαf（x）+cosα=0有四个不等实根，sinα﹣cosα≥λ恒成立，则实数λ的最大值为（ ）
A.﹣ 
B.﹣ 
C.﹣ 
D.﹣1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某校矩形的航天知识竞赛中，参与竞赛的文科生与理科生人数之比为1：3，且成绩分布在
范围内，规定分数在80以上（含80）的同学获奖，按文理科用分层抽样的放发抽取200人的成绩作为样本，得到成绩的频率分布直方图.
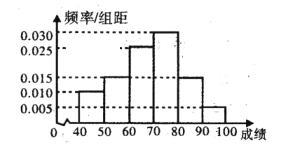
(Ⅰ)填写下面
的列联表，能否有超过95%的把握认为“获奖与学生的文理科有关”；
(Ⅱ)将上述调查所得的频率视为概率，现从参赛学生中，任意抽取3名学生，记“获奖”学生人数为
,求的分布列及数学期望.
附表及公式：
，其中
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合
为下述条件的函数
的集合：①定义域为
；②对任意实数
，都有
．
（1）判断函数
是否为中元素，并说明理由；
（2）若函数是奇函数，证明：
；
（3）设和
都是中的元素，求证：
也是中的元素，并举例说明，
不一定是中的元素．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
