
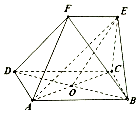
 如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF
如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF分析 (Ⅰ)如图,取AD的中点M,连接MF,OM.欲证明OE∥平面ADF,只需推知OE∥MF即可;
(Ⅱ)根据平面与平面垂直的判定定理进行证明即可.
解答 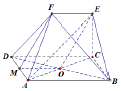 证明:(Ⅰ)如图,取AD的中点M,连接MF,OM,
证明:(Ⅰ)如图,取AD的中点M,连接MF,OM,
因为ABCD为矩形,O为BD的中点,
所以OM∥AB,AB=2OM.
又因为CE⊥平面ABCD,
所以CE⊥CD.因为CDEF为梯形,
所以CD∥EF,
又因为AB=2EF,
所以EF∥OM,EF=OM,
所以EFMO为平行四边形,
所以OE∥MF,
又MF?ADF,所以OE∥平面ADF.
(Ⅱ)因为ABCD为正方形,O为BD的中点,
所以BD⊥AC,
又因为CE⊥平面ABCD,
所以BD⊥CE,
所以BD⊥平面ACE,
所以平面BDF⊥平面ACE.
点评 此题考查立体几何中直线与平面的位置关系,面面垂直问题,考查了空间想象能力.


科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{2n-4}{3^n}$ | B. | ${a_n}=\frac{1}{{n({n+1})}}({n∈{N^*}})$ | C. | ${a_n}=\frac{1}{2n}$ | D. | ${a_n}=\frac{2}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )| A. | 9 | B. | 21 | C. | 25 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<1} | B. | {x|-1<x<3}. | C. | {x|x<-3或x>1} | D. | {x|x<-1或x>3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com