
| A. | ${a_n}=\frac{2n-4}{3^n}$ | B. | ${a_n}=\frac{1}{{n({n+1})}}({n∈{N^*}})$ | C. | ${a_n}=\frac{1}{2n}$ | D. | ${a_n}=\frac{2}{n}$ |
分析 数列{an}中,前n项和为Sn,由a1=$\frac{1}{2}$,Sn=n2an(n∈N*),可得S1;由S2可得a2的值,从而得S2;同理可得S3;可以猜想此数列的通项公式.
解答 解:在数列{an}中,前n项和为Sn,且a1=$\frac{1}{2}$,Sn=n2an(n∈N*),
∴S1=a1=$\frac{1}{2}$=$\frac{1}{1×2}$;
∴S2=$\frac{1}{2}$+a2=4a2,
∴a2=$\frac{1}{6}$=$\frac{1}{2×3}$,
∴S3=$\frac{2}{3}$+a3=9a3,
∴a3=$\frac{1}{12}$=$\frac{1}{3×4}$;
…
∴猜想此数列的通项公式an=$\frac{1}{n(n+1)}$,
故选:B
点评 本题考查了用递推公式,通过归纳推理,求数列的前n项和为Sn,需要有一定的计算能力和归纳猜想能力.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
| 支持 | 不支持 | 合计 | |
| 年龄不大于50岁 | 20 | 60 | 80 |
| 年龄大于50岁 | 10 | 10 | 20 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.100 | 0.050 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y+3)2=5 | B. | (x-2)2+(y+3)2=21 | C. | (x-2)2+(y+3)2=13 | D. | (x-2)2+(y+3)2=52 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知定义在[-2,2]上的函数y=f(x)和 y=g(x),其图象如图所示:给出下列四个命题:
已知定义在[-2,2]上的函数y=f(x)和 y=g(x),其图象如图所示:给出下列四个命题:| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
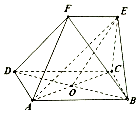 如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF
如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com