
| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
���� ���õ����ֱ��������f��x����g��x����������ڵ����䣬Ȼ������F��x��=f��x+3��•g��x-4��������������䣬����f��x+3��������g��x-4��������������䣬����ͼ��ƽ�Ƽ�����ý����
��� �⣺��f��0��=1��0��f��-1��=1-1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$��+$\frac{1}{2015}$��0��
�ຯ��f��x�������䣨-1��0��������㣻
��x�ʣ�-1��0��ʱ��f�䣨x��=$\frac{1{+x}^{2015}}{1+x}$��0��
�ຯ��f��x�������䣨-1��0���ϵ���������
�ʺ���f��x����Ψһ���x�ʣ�-1��0����
��g��1��=1-1+$\frac{1}{2}$-$\frac{1}{3}$+��-$\frac{1}{2015}$��0��g��2��=1-2+$\frac{{2}^{2}}{2}$-$\frac{{2}^{3}}{3}$+��+$\frac{{2}^{2014}}{2014}$-$\frac{{2}^{2015}}{2015}$��0��
��x�ʣ�1��2��ʱ��g�䣨x��=-1+x-x2+x3-��+x2013-x2014=$\frac{{x}^{2014}-1}{x+1}$��0��
�ຯ��g��x�������䣨1��2���ϵ����������ʺ���g��x����Ψһ���x�ʣ�1��2����
��F��x��=f��x+3��•g��x-4�����Һ���F��x��������������[a��b]��a��b��a��b��Z���ڣ�
��f��x+3��������ڣ�-4��-3���ڣ�g��x-4��������ڣ�5��6���ڣ�
���F��x��=f��x+3��•g��x-3��������������[-4��6]�ڣ�
��b-a����СֵΪ10��
��ѡ��C��
���� ���⿼���˺��������ж����������õ����о������ĵ������Լ�����������⣬Ҳ�����˺���ͼ���ƽ�����⣬�����˷�������˼�룬�Լ����Ӧ��֪ʶ�����������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 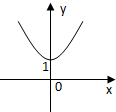 | B�� | 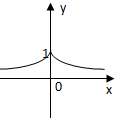 | C�� |  | D�� | 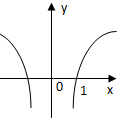 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12e | B�� | 12e2 | C�� | 24e | D�� | 24e2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{2}$ | B�� | $\frac{2��}{3}$ | C�� | $\frac{5��}{6}$ | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1-i | B�� | 1+i | C�� | 2-2i | D�� | 2+2i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �α����ܹ�ƽ����������������ļ������壺$\overrightarrow a•\overrightarrow b$����$\overrightarrow a$�ij���$|{\overrightarrow a}|$��$\overrightarrow b$��$\overrightarrow a$�����ϵ�ͶӰ$|{\overrightarrow b}|cos��\overrightarrow a��\overrightarrow b��$�ij˻������ü������壬��ʱ�ܵõ�������Ľ���˼·�����磺�߳�Ϊ1����������ABCDEF�У���P�����������ڵ�һ�㣨���߽磩����$\overrightarrow{AP}•\overrightarrow{AB}$��ȡֵ��Χ��$[{-\frac{1}{2}��\frac{3}{2}}]$��
�α����ܹ�ƽ����������������ļ������壺$\overrightarrow a•\overrightarrow b$����$\overrightarrow a$�ij���$|{\overrightarrow a}|$��$\overrightarrow b$��$\overrightarrow a$�����ϵ�ͶӰ$|{\overrightarrow b}|cos��\overrightarrow a��\overrightarrow b��$�ij˻������ü������壬��ʱ�ܵõ�������Ľ���˼·�����磺�߳�Ϊ1����������ABCDEF�У���P�����������ڵ�һ�㣨���߽磩����$\overrightarrow{AP}•\overrightarrow{AB}$��ȡֵ��Χ��$[{-\frac{1}{2}��\frac{3}{2}}]$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
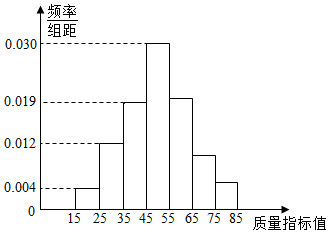 ��ij��ҵ������ij�ֲ�Ʒ�г�ȡ100����������Щ��Ʒ������ָ��ֵ���ɲ�������õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ָ��ֵ��������[55��65����[65��75����[75��85]�ڵ�Ƶ��֮��Ϊ4��2��1��
��ij��ҵ������ij�ֲ�Ʒ�г�ȡ100����������Щ��Ʒ������ָ��ֵ���ɲ�������õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ָ��ֵ��������[55��65����[65��75����[75��85]�ڵ�Ƶ��֮��Ϊ4��2��1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com