Question

如图，有一块边长为15 cm的正方形铁皮，将其四个角各截去一个边长为x cm的小正方形，然后折成一个无盖的盒子．

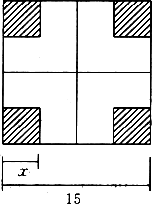
(1)求出盒子的体积y以x为自变量的函数解析式，并讨论这个函数的定义域；

(2)如果要做一个容积是150 cm³的无盖盒子，那么截去的小正方形的边长x是多少(精确到0.1 cm)？

Answer 1

答案：
解析：

解：(1)盒子的体积y是以x为自变量的函数． 　　解析式为：y＝(15－2x)2·x，x∈(0，7.5)． 　　(2)如果要做成一个容积是150 cm3的无盖盒子，那么有方程(15－2x)2·x＝150． 　　下面用二分法来求方程在(0，7.5)内的近似解． 　　令f(x)＝(15－2x)2x－150，由计算器可以确定f(x)分别在(0，1)和(4，5)内各有一个零点，即方程(15－2x)2·x＝150分别在区间(0，1)和(4，5)内各有一个解． 　　取区间(0，1)的中点x1＝0.5，计算得f(0.5)＝－52，所以零点x0∈(0.5，1)． 　　再取(0.5，1)的中点x2＝0.75，计算得f(0.75)≈－13.31，所以x0∈(0.75，1)． 　　同理可得x0∈(0.75，0.875)；x0∈(0.812 5，0.875)；x0∈(0.843 75，0.875)； 　　x0∈(0.843 75，0.859 375)；x0∈(0.843 75，0.851 562 5)；x0∈(0.843 75，0.847 656 25)． 　　所以方程在区间(0.1)内精确到0.1的近似解为0.8．同理可得方程在区间(4，5)内精确到0.1的近似值为4.7，所以要做成一个容积为150 cm3的无盖盒子时，截去小正方形的边长大约是0.8 cm或4.7 cm．

提示：

本题是用二分法来解决实际问题的例子，在遇到高次方程或较复杂的指数、对数方程的数学模型时，在一定的误差范围内可用二分法．