
已知函数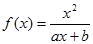 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(1)求函数f(x)的解析式;
(2)求函数 的值域.
的值域.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数  的定义域是
的定义域是  ,
,  是
是  的导函数,且
的导函数,且  在
在 上恒成立
上恒成立
(Ⅰ)求函数 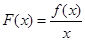 的单调区间。
的单调区间。
(Ⅱ)若函数 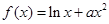 ,求实数a的取值范围
,求实数a的取值范围
(Ⅲ)设 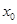 是
是  的零点 ,
的零点 , 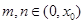 ,求证:
,求证: 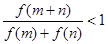 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且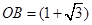 百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设
百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设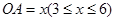 百米,
百米, 百米.
百米.
(1)试将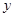 表示成
表示成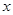 的函数,并求出函数
的函数,并求出函数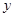 的解析式;
的解析式;
(2)当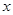 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积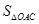 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)= 在(0,1]上解的个数.
在(0,1]上解的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com