
【题目】记关于x的不等式 ![]() 的解集为P,不等式|x+2|<3的解集为Q
的解集为P,不等式|x+2|<3的解集为Q
(1)若a=3,求P;
(2)若P∪Q=Q,求正数a的取值范围.
【答案】
(1)解:a=3时, ![]() 即
即 ![]() ,化简得
,化简得 ![]()
∴集合 ![]() ,根据分式不等式的解法,解得﹣1<x<3
,根据分式不等式的解法,解得﹣1<x<3
由此可得,集合P=(﹣1,3)
(2)解:Q={x||x+2|<3}={x|﹣3<x+2<3}={x|﹣5<x<1}
可得Q=(﹣5,1)
∵a>0,∴P={ ![]() }=(﹣1,a),
}=(﹣1,a),
又∵P∪Q=Q,得PQ,
∴(﹣1,a)(﹣5,1),由此可得0<a≤1
即正数a的取值范围是(0,1].
【解析】(1)当a=3时,解分式不等式得到集合P,(2)解绝对值不等式得到集合Q,再通过并集运算得到a的取值范围.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).


科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为{x|x∈R,且x≠2},且y=f(x+2)是偶函数,当x<2时,f(x)=|2x﹣1|,那么当x>2时,函数f(x)的递减区间是( )
A.(3,5)
B.(3,+∞)
C.(2,+∞)
D.(2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )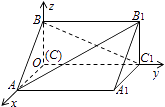
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,函数
,函数 ![]() ,其中a为常数且a>0,令函数f(x)=g(x)h(x).
,其中a为常数且a>0,令函数f(x)=g(x)h(x).
(1)求函数f(x)的表达式,并求其定义域;
(2)当 ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(3)是否存在自然数a,使得函数f(x)的值域恰为 ![]() ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市上年度电价为0.80元/千瓦时,年用电量为a千瓦时.本年度计划将电价降到0.55元/千瓦时~0.75元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时)经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为0.2a.试问当地电价最低为多少时,可保证电力部门的收益比上年度至少增加20%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点. 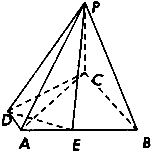
(1)求证:平面PDE⊥平面PAC;
(2)求直线PC与平面PDE所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是(﹣∞,+∞)上的奇函数,且f(x+2)=﹣f(x),当0≤x≤1时,f(x)=x.
(1)求f(π)的值;
(2)求﹣1≤x≤3时,f(x)的解析式;
(3)当﹣4≤x≤4时,求f(x)=m(m<0)的所有实根之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com