
【题目】已知函数y=f(x)的定义域为{x|x∈R,且x≠2},且y=f(x+2)是偶函数,当x<2时,f(x)=|2x﹣1|,那么当x>2时,函数f(x)的递减区间是( )
A.(3,5)
B.(3,+∞)
C.(2,+∞)
D.(2,4]
【答案】D
【解析】解:∵y=f(x+2)是偶函数,∴f(﹣x+2)=f(x+2),
则函数f(x)关于x=2对称,
则f(x)=f(4﹣x).
若x>2,则4﹣x<2,
∵当x<2时,f(x)=|2x﹣1|,
∴当x>2时,f(x)=f(4﹣x)=|24﹣x﹣1|,
则当x≥4时,4﹣x≤0,24﹣x﹣1≤0,
此时f(x)=|24﹣x﹣1|=1﹣24﹣x=1﹣16 ![]() ,此时函数递增,
,此时函数递增,
当2<x≤4时,4﹣x>0,24﹣x﹣1>0,
此时f(x)=|24﹣x﹣1|=24﹣x﹣1=16 ![]() ﹣1,此时函数递减,
﹣1,此时函数递减,
所以函数的递减区间为(2,4],
所以答案是:D.
【考点精析】通过灵活运用函数奇偶性的性质和奇偶性与单调性的综合,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则 ![]() ”,若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则
”,若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则 ![]() =( )
=( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)在(0,+∞)内单调递增且f(2)=0,则不等式 ![]() 的解集为( )
的解集为( )
A.(﹣∞,﹣2)∪(0,1)∪(1,2)
B.(﹣2,0)∪(1,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣∞,﹣2)∪(0,1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式x2+mx+3≤0的解集为A=[1,n],集合B={x|x2﹣ax+a≤0}.
(1)求m﹣n的值;
(2)若A∪B=A,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() 的定义域为集合A,B={x∈Z|0<x<10},C={x∈R|2a+3<x<a+5}.
的定义域为集合A,B={x∈Z|0<x<10},C={x∈R|2a+3<x<a+5}.
(1)求A,(RA)∩B;
(2)若A∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() +lg(x﹣1)+(x﹣3)0 的定义域为( )
+lg(x﹣1)+(x﹣3)0 的定义域为( )
A.{x|1<x≤4}
B.{x|1<x≤4且x≠3}
C.{x|1≤x≤4且x≠3}
D.{x|x≥4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 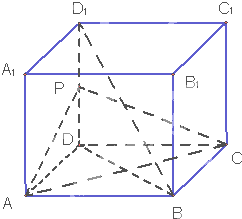
(1)求证:直线BD1∥平面PAC;
(2)求证:平面PAC⊥平面BDD1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com