Question

【题目】设f（x）是（﹣∞，+∞）上的奇函数，且f（x+2）=﹣f（x），当0≤x≤1时，f（x）=x．
（1）求f（π）的值；
（2）求﹣1≤x≤3时，f（x）的解析式；
（3）当﹣4≤x≤4时，求f（x）=m（m＜0）的所有实根之和．

Answer 1

【答案】
（1）解：∵f（x+2）=﹣f（x），

∴f（x+4）=﹣f（x+2）=f（x），

即函数f（x）是周期为4的周期函数，

则f（π）=f（π﹣4）=﹣f（4﹣π）=﹣（4﹣π）=π﹣4

（2）解：若﹣1≤x≤0，则0≤﹣x≤1，

则f（﹣x）=﹣x，

∵f（x）是奇函数，∴f（﹣x）=﹣x=﹣f（x），

即f（x）=x，﹣1≤x≤0，

即当﹣1≤x≤1时，f（x）=x，

若1≤x≤3，则﹣1≤x﹣2≤1，

∵f（x+2）=﹣f（x），

∴f（x）=﹣f（x﹣2）=﹣（x﹣2）=﹣x+2，

即当﹣1≤x≤3时，f（x）的解析式为f（x）=

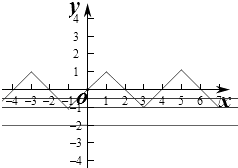
（3）解：作出函数f（x）在﹣4≤x≤4时的图象如图，

则函数的最小值为﹣1，

若m＜﹣1，则方程f（x）=m（m＜0）无解，

若m=﹣1，则函数在﹣4≤x≤4上的零点为x=﹣1，x=3，则﹣1+3=2，

若﹣1＜m＜0，则函数在﹣4≤x≤4上共有4个零点，则它们分别关于x=﹣1和x=3对称，

设分别为a，b，c，d，

则a+b=﹣2，b+d=6，

即a+b+c+d=﹣2+6=4．

【解析】（1）由f（x+2）=﹣f（x），可得f（x+4）=﹣f（x+2）=f（x），即f（x）为周期为4的周期函数，即f（π）=π-4，（2）结合分段函数和函数的奇偶性可得出每段的解析式，（3）作出f（x）在﹣4≤x≤4的图像，应用数形结合，根据对称性不难得出所有实根之和为4.
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案，需要熟知在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．