
【题目】某几何体的三视图如图所示,记A为此几何体所有棱的长度构成的集合,则( ) 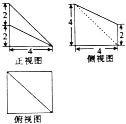
A.3∈A
B.5∈A
C.2 ![]() ∈A
∈A
D.4 ![]() ∈A
∈A
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式an=5﹣n,其前n项和为Sn , 将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn , 若存在m∈N* , 使对任意n∈N* , 总有Sn<Tn+λ恒成立,则实数λ的取值范围是( )
A.λ≥2
B.λ>3
C.λ≥3
D.λ>2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点C在椭圆M: ![]() =1(a>b>0)上,若点A(﹣a,0),B(0,
=1(a>b>0)上,若点A(﹣a,0),B(0, ![]() ),且
),且 ![]() =
= ![]()
![]() .
.
(1)求椭圆M的离心率;
(2)设椭圆M的焦距为4,P,Q是椭圆M上不同的两点.线段PQ的垂直平分线为直线l,且直线l不与y轴重合.
①若点P(﹣3,0),直线l过点(0,﹣ ![]() ),求直线l的方程;
),求直线l的方程;
②若直线l过点(0,﹣1),且与x轴的交点为D.求D点横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 与常数
与常数![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“P数对”,设函数
的一个“P数对”,设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 。
。
(1)若![]() 是
是![]() 的一个“P数对”,且
的一个“P数对”,且![]() ,求常数
,求常数![]() 的值;
的值;
(2)若(1,1)是![]() 的一个“P数对”,且
的一个“P数对”,且![]() 在
在![]() 上单调递增,求函数
上单调递增,求函数![]() 在
在![]() 上的最大值与最小值;
上的最大值与最小值;
(3)若(-2,0)是![]() 的一个“P数对”,且当
的一个“P数对”,且当![]() 时,
时,![]() ,求k的值及
,求k的值及![]() 在区间
在区间![]() 上的最大值与最小值。
上的最大值与最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾影响人们的身体健康,越来越多的人开始关心如何少产生雾霾,春节前夕,某市健康协会为了了解公众对“适当甚至不燃放烟花爆竹”的态度,随机采访了50人,将凋查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 12 | 7 | 3 | 3 |
(1)以赞同人数的频率为概率,若再随机采访3人,求至少有1人持赞同态度的概率;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(-x-1)=f(x-1),其图象过点(0,1),且与x轴有唯一交点。
(1)求f(x)的解析式;
(2)设函数g(x)=f(x)-(2+a)x,求g(x)在[1,2]上的最小值h(a)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是几何体的平面展开图,其中四边形ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面4个结论:
①直线BE与直线CF共面;②直线BE与直线AF异面;
③直线EF∥平面PBC;④平面BCE⊥平面PAD.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com