
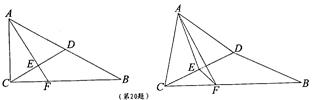
 中,
中, ,
, ,
,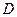 、
、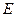 分别为
分别为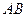 、
、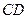 的中点,
的中点,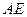 的延长线交
的延长线交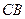 于
于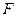 。现将
。现将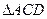 沿
沿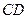 折起,折成二面角
折起,折成二面角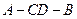 ,连接
,连接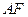 .
. :平面
:平面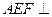 平面
平面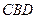 ;
;
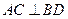 时,求二面角
时,求二面角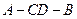 大小的余弦值.
大小的余弦值. ,
,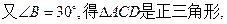 又E是CD的中点,得AF⊥CD. …………
又E是CD的中点,得AF⊥CD. ………… ..3分
..3分 CD,又AE∩EF=E
CD,又AE∩EF=E ,AE
,AE 平
平 面AED,EF
面AED,EF 平面AEF,
平面AEF, 平面CDB,故平面AEF⊥平面CBD. …………5分
平面CDB,故平面AEF⊥平面CBD. …………5分 过E与AH平行的直线为z轴
过E与AH平行的直线为z轴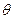 ,并设AC=
,并设AC= 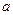 ,可得
,可得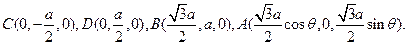 …………8分
…………8分
|
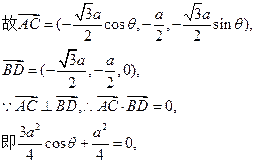 得
得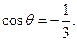
 …………11分
…………11分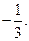 …………12分
…………12分

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
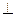 底面ABCD,
底面ABCD,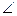 DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.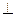 平面BEF;
平面BEF;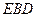 与平面
与平面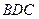 的夹角大于
的夹角大于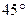 ,求k的取值范围.
,求k的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
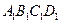 ,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.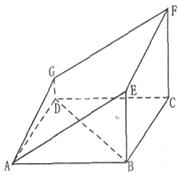

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
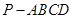 中,底面
中,底面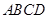 是直角梯形,
是直角梯形,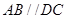 ,
,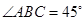 ,
,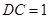 ,
,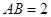 ,
,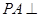 平面
平面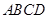 ,
,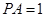 .
. 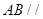 平面
平面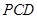 ;
;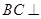 平面
平面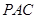 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
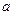 的
的 别是棱BB1、CC1、DD1的中点。
别是棱BB1、CC1、DD1的中点。
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
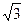 ,两个平面分别截球面得到两个圆⊙O1与⊙O2,若
,两个平面分别截球面得到两个圆⊙O1与⊙O2,若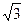 ,∠O1OO2=60°,则⊙O1与⊙O2的公共弦长为 。
,∠O1OO2=60°,则⊙O1与⊙O2的公共弦长为 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com