
若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤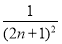 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<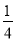 .
.
(1)不是(2)见解析
【解析】g(x)=sin x是R上的“平缓函数”,但h(x)=x2-x不是区间R上的“平缓函数”.设φ(x)=x-sin x,则φ′(x)=1-cos x≥0,则φ(x)=x-sin x是实数集R上的增函数,
不妨设x1<x2,则φ(x1)<φ(x2),即x1-sin x1<x2-sin x2,
则sin x2-sin x1<x2-x1.①
又y=x+sin x也是R上的增函数,则x1+sin x1<x2+sin x2,
即sin x2-sin x1>x1-x2,②
由①②得-(x2-x1)<sin x2-sin x1<x2-x1.
∴|sin x2-sin x1|<|x2-x1|对x1<x2都成立.
当x1>x2时,同理有|sin x2-sin x1|<|x2-x1|成立.
又当x1=x2时,|sin x2-sin x1|=|x2-x1|=0,
∴对任意的实数x1,x2∈R,
均有|sin x2-sin x1|≤|x2-x1|.
∴g(x)=sin x是R上的“平缓函数”.
∵|h(x1)-h(x2)|=|(x1-x2)(x1+x2-1)|,
取x1=3,x2=2,则|h(x1)-h(x2)|=4>|x1-x2|,
∴h(x)=x2-x不是R上的“平缓函数”.
(2)证明 由(1)得g(x)=sin x是R上的“平缓函数”.
则|sin xn+1-sin xn|≤|xn+1-xn|,
∴|yn+1-yn|≤|xn+1-xn|.
而|xn+1-xn|≤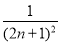 ,
,
∴|yn+1-yn|≤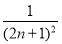 <
<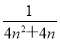 =
=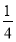
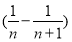 .
.
∵|yn+1-y1|=|(yn+1-yn)+(yn-yn-1)+(yn-1-yn-2)+…+(y2-y1)|,
∴|yn+1-y1|≤|yn+1-yn|+|yn-yn-1|+|yn-1-yn-2|+…+|y2-y1|.
∴|yn+1-y1|≤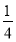
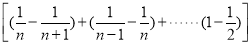
=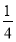
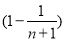 <
<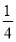 .
.


科目:高中数学 来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(解析版) 题型:选择题
长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( ).
A. 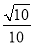 B.
B. 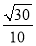 C.
C. 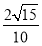 D.
D. 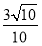
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习3-1三角函数与三角恒等变换练习卷(解析版) 题型:解答题
已知向量a=(3sin α,cos α),b=(2sin α,5sin α-4cos α),α∈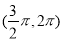 ,且a⊥b.
,且a⊥b.
(1)求tan α的值;
(2)求cos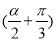 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:选择题
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围是 ( ).
A. 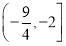 B.[-1,0] C.(-∞,-2] D.
B.[-1,0] C.(-∞,-2] D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习1-2算法与程序框图等练习卷(解析版) 题型:选择题
已知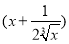 n(n∈N*)的展开式中,前三项系数成等差数列,则展开式中的常数项是 ( ).
n(n∈N*)的展开式中,前三项系数成等差数列,则展开式中的常数项是 ( ).
A.28 B.70 C. 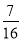 D.
D. 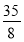
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-5练习卷(解析版) 题型:解答题
设不等式|2x-1|<1的解集为M.
(1)求集合M;
(2)若a,b∈M,试比较ab+1与a+b的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(解析版) 题型:选择题
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( ).
A.θ=0(ρ∈R)和ρcosθ=2 B.θ=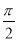 (ρ∈R)和ρcos θ=2
(ρ∈R)和ρcos θ=2
C.θ=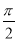 (ρ∈R)和ρcos θ=1 D.θ=0(ρ∈R)和ρcos θ=1
(ρ∈R)和ρcos θ=1 D.θ=0(ρ∈R)和ρcos θ=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(解析版) 题型:选择题
在长为12 cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小于32 cm2的概率为( ).
A.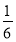 B.
B.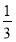 C.
C.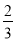 D.
D.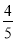
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com