
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[0,1].
(1)求函数g(x)的解析式;
(2)判断g(x)在区间[0,1]上的单调性,并用定义证明;
(3)求函数g(x)的值域.
解析: (1)因为f(a+2)=18,
所以3a+2=18,3a=2,g(x)=3ax-4x=2x-4x.
(2)函数g(x)在[0,1]上单调递减.
证明如下:设任意的0≤x1<x2≤1,
则g(x1)-g(x2)=-4x1+2x1+4x2-2x2
=(2x1-2x2)[1-(2x1+2x2)].
因为2x1-2x2<0,2x1+2x2>1,所以1-(2x1+2x2)<0,
所以g(x1)-g(x2)>0,即g(x1)>g(x2),
所以g(x)在区间[0,1]上是减函数.
(3)由(2)可知,函数g(x)在区间[0,1]上是减函数,所以g(1)≤g(x)≤g(0),又因为g(0)=-40+20=0,g(1)=-4+2=-2,所以g(x)∈[-2,0].


科目:高中数学 来源: 题型:
下列各式错误的是( )
A.30.8>30.7 B.log0.50.4>log0.50.6
C.0.75-0.2<0.750.2 D.lg 1.6>lg 1.3
查看答案和解析>>
科目:高中数学 来源: 题型:
某天0时,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常(正常体温约为37 ℃),但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了.下面能大致反映出小鹏这一天(0时至24时)体温变化情况的图象是( )
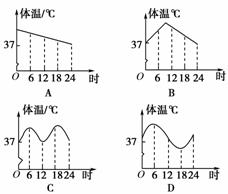
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系).根据图象提供的信息解答下列问题:
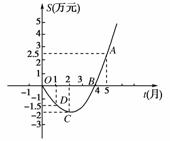
(1)由已知图象上的三点坐标,求累积利润S(万元)与时间t(月)之间的函数关系式;
(2)求截止到第几月末公司累积利润可达到30万元;
(3)求第八个月公司所获利润是多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com