
已知函数 .
.
(1)若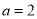 ,求曲线
,求曲线 在点
在点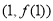 处的切线方程;
处的切线方程;
(2)求函数 的单调区间;
的单调区间;
(3)设函数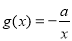 .若至少存在一个
.若至少存在一个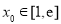 ,使得
,使得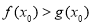 成立,求实数
成立,求实数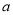 的取值范围.
的取值范围.
(1)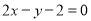 ,(2)当
,(2)当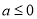 时,
时,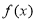 在
在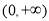 上单调递减,若
上单调递减,若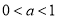 ,单调递增区间为
,单调递增区间为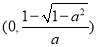 和
和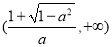 ,单调递减区间为
,单调递减区间为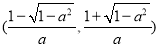 .若
.若 ,在
,在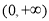 上单调递增.(3)
上单调递增.(3) .
.
【解析】
试题分析:(1)利用导数几何意义求切线斜率,根据点斜式写切线过程. 函数的定义域为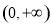 ,
,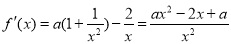 .当
.当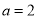 时,函数
时,函数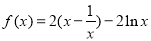 ,
,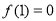 ,
,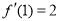 .所以曲线
.所以曲线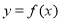 在点
在点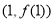 处的切线方程为
处的切线方程为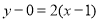 ,即
,即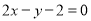 .(2)利用导数研究函数单调性,关键明确导函数零点与定义域的关系,正确判断导数符号. 当
.(2)利用导数研究函数单调性,关键明确导函数零点与定义域的关系,正确判断导数符号. 当 时,
时,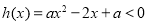 ,
,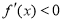 ,当
,当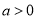 时,若
时,若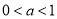 ,由
,由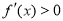 ,即
,即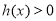 ,得
,得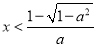 或
或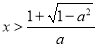 ;由
;由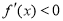 ,即
,即 ,得
,得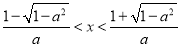 .若
.若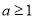 ,
, ,
,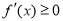 .(3)存在性问题,利用变量分离转化为求函数最值. 因为
.(3)存在性问题,利用变量分离转化为求函数最值. 因为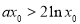 ,等价于
,等价于 .令
.令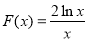 ,等价于“当
,等价于“当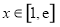 时,
时, ”. 因为当
”. 因为当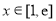 时,
时,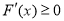 ,所以
,所以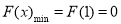 ,因此
,因此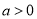 .
.
函数的定义域为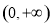 ,
,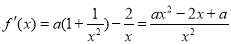 . 1分
. 1分
(1)当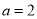 时,函数
时,函数 ,
,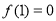 ,
,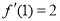 .
.
所以曲线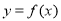 在点
在点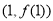 处的切线方程为
处的切线方程为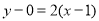 ,
,
即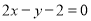 . 4分
. 4分
(2)函数 的定义域为
的定义域为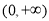 .
.
1.当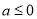 时,
时,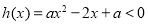 在
在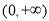 上恒成立,
上恒成立,
则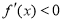 在
在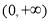 上恒成立,此时
上恒成立,此时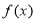 在
在 上单调递减. 5分
上单调递减. 5分
2.当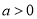 时,
时,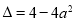 ,
,
(ⅰ)若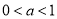 ,
,
由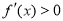 ,即
,即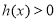 ,得
,得 或
或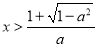 ; 6分
; 6分
由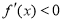 ,即
,即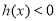 ,得
,得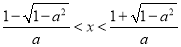 . 7分
. 7分
所以函数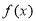 的单调递增区间为
的单调递增区间为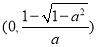 和
和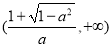 ,
,
单调递减区间为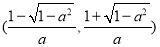 . 9分
. 9分
(ⅱ)若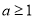 ,
,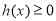 在
在 上恒成立,则
上恒成立,则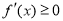 在
在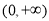 上恒成立,此时
上恒成立,此时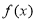 在
在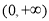 上单调递增. 10分
上单调递增. 10分
(3)因为存在一个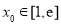 使得
使得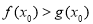 ,
,
则 ,等价于
,等价于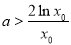 . 12分
. 12分
令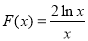 ,等价于“当
,等价于“当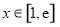 时,
时,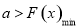 ”.
”.
对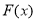 求导,得
求导,得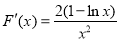 . 13分
. 13分
因为当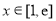 时,
时,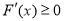 ,所以
,所以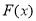 在
在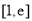 上单调递增.
上单调递增.
所以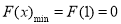 ,因此
,因此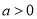 . 16分
. 16分
另【解析】
设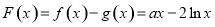 ,定义域为
,定义域为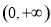 ,
,
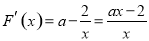 .
.
依题意,至少存在一个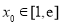 ,使得
,使得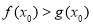 成立,
成立,
等价于当 时,
时,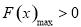 . 11分
. 11分
(1)当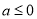 时,
时,
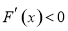 在
在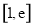 恒成立,所以
恒成立,所以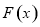 在
在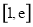 单调递减,只要
单调递减,只要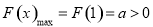 ,
,
则不满足题意. 12分
(2)当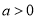 时,令
时,令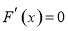 得
得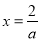 .
.
(ⅰ)当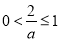 ,即
,即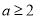 时,
时,
在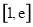 上
上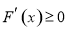 ,所以
,所以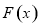 在
在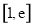 上单调递增,
上单调递增,
所以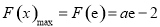 ,由
,由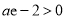 得,
得,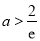 ,所以
,所以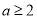 . 13分
. 13分
(ⅱ)当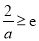 ,即
,即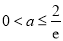 时,
时,
在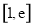 上
上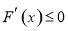 ,所以
,所以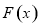 在
在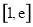 单调递减,
单调递减,
所以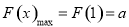 ,由
,由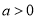 得
得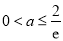 . 14分
. 14分
(ⅲ)当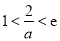 ,即
,即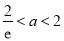 时, 在
时, 在 上
上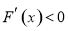 ,在
,在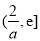 上
上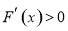 ,
,
所以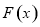 在
在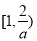 单调递减,在
单调递减,在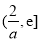 单调递增,
单调递增,
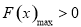 ,等价于
,等价于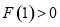 或
或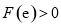 ,解得
,解得 ,所以,
,所以,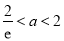 . 15分
. 15分
综上所述,实数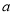 的取值范围为
的取值范围为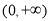 . 16分
. 16分
考点:利用导数求切线方程,利用导数求函数单调区间,利用导数求函数最值


科目:高中数学 来源:2015届江苏省泰州市姜堰区高二下学期期中考试文科数学试卷(解析版) 题型:填空题
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂
巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,
以 表示第
表示第 幅图的蜂巢总数,则
幅图的蜂巢总数,则 =_______.
=_______.

查看答案和解析>>
科目:高中数学 来源:2015届江苏省泰州市姜堰区高二下学期期中考试文科数学试卷(解析版) 题型:填空题
“ ”是“
”是“ ”的 条件. (请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空
”的 条件. (请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空
查看答案和解析>>
科目:高中数学 来源:2015届江苏省五校高二下学期期中理科数学试卷(解析版) 题型:填空题
5名男性驴友到某旅游风景区游玩,晚上入住一家宾馆,宾馆有3间客房可选,一间客房为3人间,其余为2人间,则5人入住两间客房的不同方法有 种(用数字作答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com