
| A. | ln(a-b)>0 | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ${(\frac{1}{4})^a}<{(\frac{1}{3})^b}$ | D. | 3a-b<1 |
分析 由题意可得a>b>0,再利用对数函数、指数函数与幂函数的单调性即可得出答案.
解答 解:∵$y=lo{g}_{\frac{1}{2}}x$是定义域上的减函数,且${log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}b$,
∴a>b>0.
当0<a-b<1时,ln(a-b)<0,
当a-b≥1时,ln(a-b)≥0,∴A错误;
∵$\frac{1}{a}-\frac{1}{b}=\frac{b-a}{ab}<0$,
∴$\frac{1}{a}<\frac{1}{b}$,B错误;
∵$y=(\frac{1}{4})^{x}$是定义域R上的减函数,
∴$(\frac{1}{4})^{a}<(\frac{1}{4})^{b}$,
又∵y=xb在(0,+∞)上是增函数,
∴$(\frac{1}{4})^{b}<(\frac{1}{3})^{b}$,
∴$(\frac{1}{4})^{a}<(\frac{1}{3})^{b}$,C正确;
∵a-b>0,∴3a-b>1,D错误.
故选:C.
点评 本题考查函数的单调性,函数值的比较,属于中档题.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 比赛项目 | 男单 | 女单 | 混双 |
| 平均比赛时间 | 25分钟 | 20分钟 | 35分钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
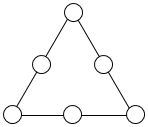 如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个.
如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | -32 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 60 | C. | 70 | D. | 210 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com