
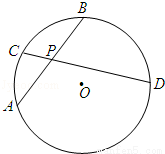
(2013•江门一模)(几何证明选讲选做题)如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为 .
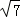
【解析】
试题分析:取CD中点M,连接OD、OM、OP、OA,可得OM⊥CD且OP⊥AB.Rt△OPA中运用勾股定理算出OA=4 ,根据相交弦定理和题中数据算出弦CD=10,从而在Rt△OMD中用勾股定理算出OM=
,根据相交弦定理和题中数据算出弦CD=10,从而在Rt△OMD中用勾股定理算出OM=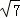 ,即得圆心O到CD的距离.
,即得圆心O到CD的距离.
【解析】
取CD中点M,连接OD、OM、OP、OA,
根据圆的性质,OM⊥CD,OM即为O到CD的距离
∵PA=PB=4,即P为AB中点,
∴OP⊥AB,可得OP=4.
Rt△OPA中,OA=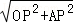 =4
=4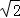
∵PA=PB=4,PD=4PC,
∴由PA•PB=PC•PD,即42=4PC2,可得PC=2
因此,PD=4PC=8,得CD=10
∴Rt△OMD中,DM= CD=5,OD=OA=4
CD=5,OD=OA=4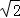
可得OM= =
=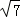
故答案为: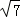



科目:高中数学 来源:[同步]2015人教B版选修4-5 3.2用数学归纳法证明不等式练习卷(解析版) 题型:选择题
用数学归纳法证明不等式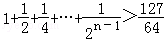 成立,起始值至少应取为( )
成立,起始值至少应取为( )
A.7 B.8 C.9 D.10
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:填空题
(2014•广东模拟)如图,在△ABC中,AB=AC,∠C=72°,⊙O过A、B两点且与BC相切于点B,与AC交于点D,连接BD,若BC=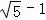 ,则AC= .
,则AC= .

查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
如图,圆内接△ABC的外角∠ACH的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BH,垂足是H,下列结论:①CH=CP;②AD=DB;③AP=BH;④DH为圆的切线.其中一定成立的是( )
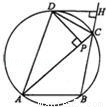
A.①②④ B.①③④ C.②③④ D.①②③
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
(2011•太原模拟)如图,过⊙O外一点P作一条直线与⊙O交于A、B两点,已知PA=2,点P到⊙O的切线长PT=4,则弦AB的长为( )
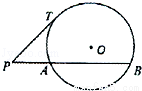
A.4 B.6 C.8 D.10
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
圆内接四边形ABCD中,cosA+cosB+cosC+cosD等于( )
A.0 B.4 C.2 D.不确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
A.120° B.100° C.80° D.60°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:选择题
i是虚数单位,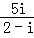 =( )
=( )
A.1+2i B.﹣1﹣2i C.1﹣2i D.﹣1+2i
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:填空题
某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距离车站10千米处建仓库,这两项费用y1和y2分别为2万元和8万元,那么,要使这两项费用之和最小,仓库应建在离车站 千米处.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com