练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，圆内接△ABC的外角∠ACH的平分线与圆交于D点，DP⊥AC，垂足是P，DH⊥BH，垂足是H，下列结论：①CH=CP；②AD=DB；③AP=BH；④DH为圆的切线．其中一定成立的是（ ）

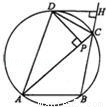
    A.①②④ B.①③④ C.②③④ D.①②③

     

    D

    【解析】

    试题分析：连接BD．证△PCD≌△HCD（HL）得CH=CP；再证明△ADP≌△BDH（AAS）得AD=DB；AP=BH，无法证明DH为圆的切线．

    【解析】
    连接BD．

    由题意可证△PCD≌△HCD（HL），

    ∴CH=CP；

    还可以证明△ADP≌△BDH（AAS），

    ∴AD=DB；AP=BH．

    因圆的直径不确定，而无法证明DH为圆的切线．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷（解析版） 题型：

    下列各点不在曲线x2+y2+z2=12上的是（ ）

    A.（2，﹣2，2） B.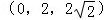

    C.（﹣2，2，2） D.（1，3，4）

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量（解析版） 题型：填空题

    矩阵的特征值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

    如图，P是半圆O的直径BC延长线上一点，PT切半圆于点T，TH⊥BC于H，若PT=1，PB+PC=2a，则PH=（ ）

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

    如图，BC是半圆O的直径，点D是半圆上一点，过点D作⊙O切线AD，BA⊥DA于点A，BA交半圆于点E．已知BC=10，AD=4．那么直线CE与以点O为圆心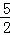，为半径的圆的位置关系是 （ ）

    A.相离 B.相交 C.相切 D.不确定

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

    （2010•自贡二模）如图，两个同心圆的半径分别为3cm和5cm，弦AB与小圆相切于点C，则AB的长为（ ）

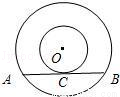
    A.4cm B.5cm C.6cm D.8cm

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理（解析版） 题型：填空题

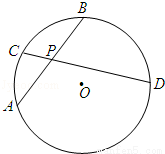
    （2013•江门一模）（几何证明选讲选做题）如图，圆O内的两条弦AB、CD相交于P，PA=PB=4，PD=4PC．若O到AB的距离为4，则O到CD的距离为 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理（解析版） 题型：选择题

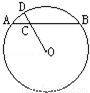
    如图，AB是⊙O的弦，C是AB的三等分点，连接OC并延长交⊙O于点D．若OC=3，CD=2，则圆心O到弦AB的距离是（ ）

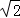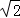    A.6 B.9﹣ C.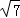 D.25﹣3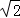

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-2 2.2直接证明与间接证明练习卷（解析版） 题型：填空题

    如果a+b＞a+b，则a、b应满足的条件是 ．

     

    查看答案和解析>>

    同步练习册答案