
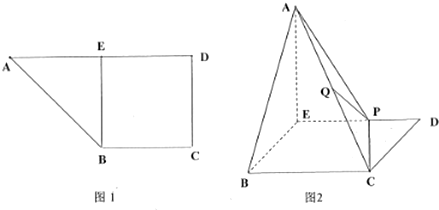
分析 (Ⅰ)根据线面平行的判定定理证明ME∥PQ即可.
(Ⅱ)建立空间坐标系,求出平面的法向量,利用向量法结合二面角的余弦值建立方程关系进行求解即可.
解答 证明:(Ⅰ)取AB的中点M,连结EM,QM.
由Q为AC的中点,得MQ∥BC,且$MQ=\frac{1}{2}BC$,
又PE∥BC,且$PE=\frac{1}{2}BC$,
∴PE∥MQ,PE=MQ,
∴四边形PEMQ为平行四边形,
故ME∥PQ.
又PQ?平面AEB,ME?平面AEB,
所以PQ∥平面AEB.
(Ⅱ)在△AEC中,AE=4,EC2=4+4=32,AC=4$\sqrt{3}$,
∴AE2+EC2=AD2,
由勾股定理得AE⊥EC,
∵AE⊥BE,CE∩BE=E,
∴AE⊥平面BCDE,
以E为原点,分别以$\overrightarrow{EB},\overrightarrow{ED},\overrightarrow{EA}$为x轴、y轴、z轴的正方向建立空间直角坐标系(如图2),
设PF=a,0≤a≤4,
则E(0,0,0),B(4,0,0),A(0,0,4),P(0,a,0),
C(4,4,0),$\overrightarrow{PC}$=(4,4-a,0),$\overrightarrow{AC}$=(4,4,-4),
设平面APC的法向量为$\overrightarrow{m}$=(x,y,z),
由$\overrightarrow{m}$•$\overrightarrow{PC}$=4x+(4-a)y=0,$\overrightarrow{m}$•$\overrightarrow{AC}$=4x+4y-4z=0,
令z=1,则x=1-$\frac{4}{a}$,y=$\frac{4}{a}$,则$\overrightarrow{m}$=(1--$\frac{4}{a}$,$\frac{4}{a}$,1)
平面AEB的一个法向量为$\overrightarrow{n}$=(0,1,0),
∵平面AEB和平面APC所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$,
∴|cos$<\overrightarrow{m},\overrightarrow{n}>$|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{\left|\overrightarrow{m}\right|\left|\overrightarrow{n}\right|}$|=$\frac{\frac{4}{a}}{\sqrt{(\frac{4}{a})^{2}+(1-\frac{4}{a})^{2}+1}}$=$\frac{\sqrt{6}}{3}$,
平方解得a=2,即PE=2.
点评 本题考查了空间中的线面平行的判定以及二面角的求解,建立空间坐标系,求出平面的法向量,利用向量法是解决本题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0<a≤$\frac{1}{e}$ | B. | a$≥\frac{1}{e}$ | C. | $\frac{1}{{e}^{2}}$<a≤$\frac{1}{e}$ | D. | a≥$\frac{1}{{e}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{11}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{5}{11}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱锥S-ABC中,已知△ABC是以角A为直角的等腰三角形,AB=2,SB=SC=$\sqrt{3}$,SO⊥BC,垂足为O.
三棱锥S-ABC中,已知△ABC是以角A为直角的等腰三角形,AB=2,SB=SC=$\sqrt{3}$,SO⊥BC,垂足为O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
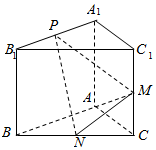 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$(λ∈R).
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$(λ∈R).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{49}$ | B. | $\frac{12}{49}$ | C. | $\frac{6}{25}$ | D. | $\frac{4}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com