
分析 (I)由椭圆的焦点在x轴上,设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),则c=$\sqrt{3}$,b2=a2-c2=3,将点($\sqrt{3},\frac{1}{2}$)代入椭圆方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-3}=1$,即可求得a和b的值,求得椭圆C的方程:
(II)D在AB的垂直平分线上,OD:$y=-\frac{1}{k}x$,将直线方程代入椭圆方程求得(1+4k2)x2=4,则|AB|=2|OA|=4$\sqrt{\frac{{{k^2}+1}}{{4{k^2}+1}}}$,|OC|=2$\sqrt{\frac{{{k^2}+1}}{{{k^2}+4}}}$,可知S△ABC=2S△OAC=|OA|×|OC|=$\frac{{4(1+{k^2})}}{{(1+4{k^2})({k^2}+4)}}$,根据基本不等式的性质可知:$\sqrt{(1+4{k^2})({k^2}+4)}≤\frac{{5(1+{k^2})}}{2}$,因此S△ABC=2S△OAC≥$\frac{8}{5}$,即可求得直线AB的方程.
解答 解:(I)由题意可知:椭圆的焦点在x轴上,设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
则c=$\sqrt{3}$,b2=a2-c2=3,
将点($\sqrt{3},\frac{1}{2}$)代入椭圆方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-3}=1$,即$\frac{3}{{a}^{2}}+\frac{1}{4({a}^{2}-3)}=1$,
解得:a2=4,b2=1,
∴椭圆C的方程:$\frac{x^2}{4}+{y^2}=1$…(4分)
(II)D在AB的垂直平分线上,
∴OD:$y=-\frac{1}{k}x$.…(5分)
由$\left\{\begin{array}{l}y=kx\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$,可得(1+4k2)x2=4,
|AB|=2|OA|=2$\sqrt{{x^2}+{y^2}}$=4$\sqrt{\frac{{{k^2}+1}}{{4{k^2}+1}}}$,…(6分)
同理可得|OD|=2$\sqrt{\frac{{{k^2}+1}}{{{k^2}+4}}}$,…(7分)
则S△ABD=2S△OAD=|OA|×|OD|=$\frac{4(1+{k}^{2})}{\sqrt{(4{k}^{2}+1)(k{{\;}^{2}+}^{\;}4)}}$.…(8分)
由于$\sqrt{(1+4{k^2})({k^2}+4)}≤\frac{{5(1+{k^2})}}{2}$,…(10分)
∴S△ABD=2S△OAD≥$\frac{8}{5}$,
当且仅当1+4k2=k2+4,即k=±1时取等号.
∴△ABD的面积取最小值$\frac{8}{5}$,直线AB的方程为y=±x.…(12分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查三角形的面积公式与基本不等式性质的应用,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
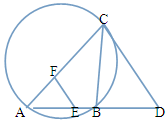 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα=$\frac{3}{5}$ | B. | cosα=-$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | tanα=-$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com