
【题目】如图,在棱长为2的正方体OABC﹣O′A′B′C′中,E,F分别是棱AB,BC上的动点. 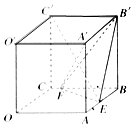
(1)当AE=BF时,求证A′F⊥C′E;
(2)若E,F分别为AB,BC的中点,求直线O′B与平面B′EF所成角的正弦值.
【答案】
(1)证明:以CC'为z轴,CO为x轴,CB为y轴建立空间直角坐标系,如图所示,
设F(0,y,0),∵AE=BF,∴BE=CF,∴E(y,2,0),
又A′(2,2,2),C′(0,0,2),
∴ ![]() =(﹣2,y﹣2,﹣2),
=(﹣2,y﹣2,﹣2), ![]() =(y,2,﹣2),
=(y,2,﹣2),
∵ ![]()
![]() =﹣2y+2y﹣4+4=0,
=﹣2y+2y﹣4+4=0,
∴ ![]() ⊥
⊥ ![]() ,∴A′F⊥C′E
,∴A′F⊥C′E
(2)证明:解:E(1,2,0),F(0,1,0),B'(0,2,2),
![]() ,
, ![]() =(0,1,2),
=(0,1,2),
设平面B'EF的法向量为 ![]() ,
,
则 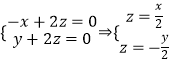 ,取x=2,则z=1,y=﹣2,
,取x=2,则z=1,y=﹣2, ![]()
又O′(2,0,2),B(0,2,0), ![]() =(﹣2,2,﹣2),
=(﹣2,2,﹣2),
设O′B与平面B′EF所成的角为θ,
则sinθ=|cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() ,
,
即直线O′B与平面B′EF所成角的正弦值为 ![]() .
.
【解析】(1)以CC'为z轴,CO为x轴,CB为y轴建立空间直角坐标系,利用向量法能证明A′F⊥C′E.(2)求出平面B'EF的法向量和 ![]() ,利用向量法能求出直线O′B与平面B′EF所成角的正弦值.
,利用向量法能求出直线O′B与平面B′EF所成角的正弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则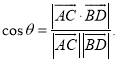 .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() .A为椭圆上异于顶点的一点,点P满足
.A为椭圆上异于顶点的一点,点P满足 ![]() =
= ![]() ,
, 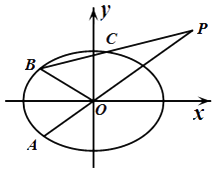
(1)若点P的坐标为(2, ![]() ),求椭圆的方程;
),求椭圆的方程;
(2)设过点P的一条直线交椭圆于B,C两点,且 ![]() =m
=m ![]() ,直线OA,OB的斜率之积﹣
,直线OA,OB的斜率之积﹣ ![]() ,求实数m的值;
,求实数m的值;
(3)在(1)的条件下,是否存在定圆M,使得过圆M上任意一点T都能作出该椭圆的两条切线,且这两条切线互相垂直?若存在,求出定圆M;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
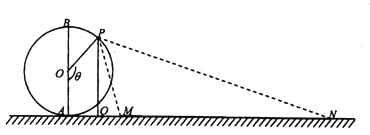
【题目】如图,摩天轮的半径![]() 为
为![]() ,它的最低点
,它的最低点![]() 距地面的高度忽略不计.地上有一长度为
距地面的高度忽略不计.地上有一长度为![]() 的景观带
的景观带![]() ,它与摩天轮在同一竖直平面内,且
,它与摩天轮在同一竖直平面内,且![]() .点
.点![]() 从最低点
从最低点![]() 处逆时针方向转动到最高点
处逆时针方向转动到最高点![]() 处,记
处,记![]() .
.
(1)当![]() 时,求点
时,求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)试确定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,经过B(1,2)作两条互相垂直的直线l1和l2 , l1交y轴正半轴于点A,l2交x轴正半轴于点C. 
(1)若A(0,1),求点C的坐标;
(2)试问是否总存在经过O,A,B,C四点的圆?若存在,求出半径最小的圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4tanxsin( ![]() ﹣x)cos(x﹣
﹣x)cos(x﹣ ![]() )﹣
)﹣ ![]() .
.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题: ①函数y=sin( ![]() ﹣2x)是偶函数;
﹣2x)是偶函数;
②方程x= ![]() 是函数y=sin(2x+
是函数y=sin(2x+ ![]() )的图象的一条对称轴方程;
)的图象的一条对称轴方程;
③若α、β是第一象限角,且α>β,则sinα>sinβ;
④设x1、x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根,则x1x2=1;
其中正确命题的序号是 . (填出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com