
| x | 2 | 3 | 5 | 6 |
| y | 3 | 5 | 7 | 9 |
分析 (1)求出x,y的平均数,得到回归系数,即可求销售额y关于广告费用x的线性回归方程;
(2)把x=8代入,能广告费用投入8万元预测销售额.
解答 解:(1)
| x | 2 | 3 | 5 | 6 |
| y | 3 | 5 | 7 | 9 |
| xiyi | 6 | 15 | 35 | 54 |
| $\overline x=4,\overline y=6$ | ||||
| $\begin{array}{l}\sum_{i=1}^n{{x_i}{y_i}}=110,n\overline x\overline y=96\\ \sum_{i=1}^n{{x_i}^2=74,n{{\overline x}^2}}=64\end{array}$ | ||||
点评 本题考查线性回归方程.考查预报变量的值,考查样本中心点的应用,本题是一个基础题.


科目:高中数学 来源: 题型:解答题
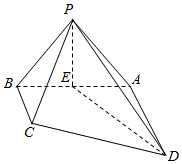 在四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC=$\frac{1}{2}$AD,E是线段AB的中点.
在四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC=$\frac{1}{2}$AD,E是线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>2 | B. | a≤2 | C. | a>1 | D. | a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 125.4 | C. | 225 | D. | 350.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com