
| A. | a>2 | B. | a≤2 | C. | a>1 | D. | a≤1 |
分析 分别求出f(x)和g(x)的值域,令g(x)的值域为f(x)的值域的子集列出不等式解出a.
解答 解:∵函数f(x)=log2(x2+2x+a),g(x)=2x,
∴当a>1时,函数f(x)的值域为[log2(a-1),+∞),
当a≤1时,函数f(x)的值域为R,
函数g(x)的值域为(0,+∞),
∵任意的实数x1,总存在x2,使得f(x2)=g(x1),
∴当a>1时,(0,+∞)⊆[log2(a-1),+∞),
∴log2(a-1)≤0,
即0<a-1≤1,
解得:1<a≤2,
当a≤1时,满足条件,
综上所述,a≤2,
故选:B.
点评 本题考查了二次函数的值域,对数函数的单调性与值域,集合间的关系,分类讨论思想,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
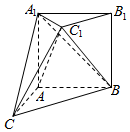 如图,在多面体ABC-A1B1C1中,四边形A1B1BA是正方形,AC=AB=1,△A1BC为等边三角形,$\overrightarrow{BC}$=2$\overrightarrow{{B}_{1}{C}_{1}}$.
如图,在多面体ABC-A1B1C1中,四边形A1B1BA是正方形,AC=AB=1,△A1BC为等边三角形,$\overrightarrow{BC}$=2$\overrightarrow{{B}_{1}{C}_{1}}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.75 | B. | 1.25 | C. | 1.75 | D. | 3.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
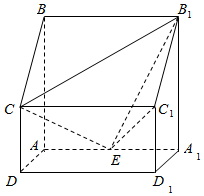 如图,四棱猪ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,A1A=AB=2,E为棱AA1的中点.
如图,四棱猪ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,A1A=AB=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,若该多面体的所有顶点都在球O的表面上,则球O的表面积是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,若该多面体的所有顶点都在球O的表面上,则球O的表面积是( )| A. | 8π | B. | 12π | C. | 16π | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 2 | 3 | 4 | 5 |
| y | 2.5 | 3 | m | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 3 | 5 | 6 |
| y | 3 | 5 | 7 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48种 | B. | 36种 | C. | 24种 | D. | 12种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com