
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题等价于g(x)在[1,2]上的最小值不大于f(x)在(0,2)上的最小值$-\frac{1}{2}$,根据函数的单调性分别求出函数g(x)的最小值和f(x)的最小值,得到关于b的不等式,解出即可.
解答 解:(1)因为$f(x)=lnx-ax+\frac{1-a}{x}-1$
所以$f'(x)=\frac{1}{x}-a+\frac{a-1}{x^2}=-\frac{{a{x^2}-x+1-a}}{x^2},x∈(0,+∞)$
令f′(x)=0,解得:x=1或$\frac{1}{a}$-1,-------------------(2分)
当0<a<$\frac{1}{2}$时,$\frac{1}{a}-1>1>0$,x∈(0,1)时,此时f'(x)<0,函数f(x)单调递减;
$x∈(1,\frac{1}{a}-1)$时,此时f'(x)>0,函数f(x)单调递增;
$x∈(\frac{1}{a}-1,+∞)$时,此时f′(x)<0,函数f(x)单调递减:-------------------(5分)
(2)因为$a=\frac{1}{4}∈(0,\frac{1}{2})$,由(I)知,$\frac{1}{a}-1=3∉(0,2)$,
当x∈(0,1)时,f'(x)<0,函数f(x)单调递减;
当x∈(1,2)时,f'(x)>0,函数f(x)单调递增,
所以f(x)在(0,2)上的最小值为$f(1)=-\frac{1}{2}$
由于“对任意x1∈(0,2),存在x2∈[1,2],
使f(x1)≥g(x2)等价于g(x)在[1,2]上的最小值不大于f(x)在(0,2)上的最小值$-\frac{1}{2}$”(*)-------------------(8分)
又g(x)=(x-b)2+4-b2,x∈[1,2],
所以①当b<1时,因为[g(x)]min=g(1)=5-2b>0此时与(*)矛盾,
②当1≤b≤2时,因为${[g(x)]_{min}}=4-{b^2}≥0$同样与(*)矛盾,
③当b>2时,因为[g(x)]min=g(2)=8-4b,
且当b>2时,8-4b<0,解不等式$8-4b≤-\frac{1}{2}$,可得$b≥\frac{17}{8}$-------------------(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查分类讨论思想,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 10 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 4 | 5 | 6 |
| y | 8 | 6 | 7 |
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
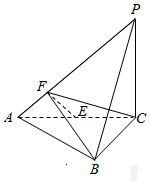 如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC,E为AC中点,EF⊥AP,垂足为F.
如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC,E为AC中点,EF⊥AP,垂足为F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
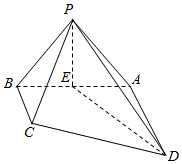 在四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC=$\frac{1}{2}$AD,E是线段AB的中点.
在四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC=$\frac{1}{2}$AD,E是线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>2 | B. | a≤2 | C. | a>1 | D. | a≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com