
| A. | 7 | B. | 8 | C. | 10 | D. | 15 |
分析 设甲桶中原有水量为a,则a-a•e5k=a•e5k,从而k=$\frac{1}{5}ln\frac{1}{2}$.再由a-a•emk=7a•emk,能求出结果.
解答 解:设甲桶中原有水量为a,
∵经过5分钟乙桶中的水量与甲桶相等,
∴由题意甲桶中共有水:a-a•e5k=a•e5k,
解得k=$\frac{1}{5}ln\frac{1}{2}$.
∵经过m分钟乙桶中的水量是甲桶的7倍,
∴a-a•emk=7a•emk,
解得emk=$\frac{1}{8}$,${e}^{\frac{m}{5}ln\frac{1}{2}}$=$\frac{1}{8}$,
解得m=15.
∴m的值为15.
故选:D.
点评 本题考查函数值的求法,是中档题,解题时要认真审题,注意函数性质在生产生活中的实际应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 5π | B. | 9π | C. | 16π | D. | 25π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 36 | C. | 40 | D. | 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
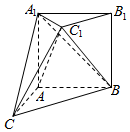 如图,在多面体ABC-A1B1C1中,四边形A1B1BA是正方形,AC=AB=1,△A1BC为等边三角形,$\overrightarrow{BC}$=2$\overrightarrow{{B}_{1}{C}_{1}}$.
如图,在多面体ABC-A1B1C1中,四边形A1B1BA是正方形,AC=AB=1,△A1BC为等边三角形,$\overrightarrow{BC}$=2$\overrightarrow{{B}_{1}{C}_{1}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com