
分析 由题意画出图形,结合向量加法法则即已知条件求值.
解答 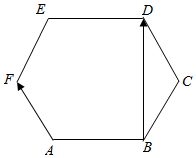 解:如图,
解:如图,
∵ABCDEF为边长是1的正六边形,
∴$|\overrightarrow{AF}|=|\overrightarrow{DC}|=1$,且<$\overrightarrow{BC},\overrightarrow{CD}$>=60°,
∴$\overrightarrow{AF}$•$\overrightarrow{BD}$=$\overrightarrow{CD}$•($\overrightarrow{BC}+\overrightarrow{CD}$)=$\overrightarrow{CD}•\overrightarrow{BC}+|\overrightarrow{CD}{|}^{2}$
=$|\overrightarrow{CD}||\overrightarrow{BC}|cos60°+|\overrightarrow{CD}{|}^{2}$=$1×1×\frac{1}{2}+1=\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查平面向量的数量积运算,考查数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{ln3}{3}$,-$\frac{ln2}{2}$] | B. | (-$\frac{1}{e}$,-$\frac{ln2}{2}$] | C. | [$\frac{ln2}{2}$,-$\frac{ln3}{3}$] | D. | [$\frac{ln2}{2}$,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:
下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | (-$\sqrt{5}$,$\sqrt{5}$) | C. | (-$\frac{\sqrt{5}}{2}$,$\frac{\sqrt{5}}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
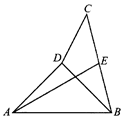 将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦为( )
将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦为( )| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{30}}}{6}$ | D. | $\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com