
���� ��1������C1�IJ���������ȥ�����ȵ�����C1����ͨ���̣���x=��cos�ȣ�y=��sin�ȣ����������C1�ļ����귽�̣�
��2�����A�ļ�����Ϊ��${��}_{1}��\frac{��}{6}$������B�ļ�����Ϊ��${��}_{2}��\frac{��}{6}$������${��}_{1}=4cos\frac{��}{6}=2\sqrt{3}$��${��}_{2}=\sqrt{3}sin\frac{��}{6}+cos\frac{��}{6}$=$\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}=\sqrt{3}$���ɴ������|AB|��
��� �⣺��1��������C1�IJ�������Ϊ$\left\{\begin{array}{l}x=2+2cos��\\ y=2sin��\end{array}\right.$����Ϊ��������
����ȥ�����ȵ�����C1����ͨ����Ϊ��x-2��2+y2=4����x2+y2-4x=0��
��x=��cos�ȣ�y=��sin�ȣ�������C1�ļ����귽��Ϊ��2=4cos�ȣ�
��2�����A�ļ�����Ϊ��${��}_{1}��\frac{��}{6}$������B�ļ�����Ϊ��${��}_{2}��\frac{��}{6}$����
��${��}_{1}=4cos\frac{��}{6}=2\sqrt{3}$��${��}_{2}=\sqrt{3}sin\frac{��}{6}+cos\frac{��}{6}$=$\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}=\sqrt{3}$��
��|AB|=|��1-��2|=$\sqrt{3}$��
���� ���⿼��ֱ�ߵļ����귽�̵��������߶γ��������鼫���귽�̡�ֱ�����귽�̡��������̵Ļ���������������֤����������������������黯����ת��˼�롢�����뷽��˼�룬���е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+y2=16 | B�� | x2+y2=16��x��4�� | C�� | x2-y2=16 | D�� | x2-y2=16��x��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��+�ޣ� | B�� | ��-�ޣ�1] | C�� | ��0��1] | D�� | ��-�ޣ�0����{1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
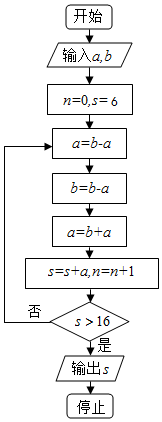
| A�� | 17 | B�� | 22 | C�� | 18 | D�� | 20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | n | B�� | n-1 | C�� | $\frac{n��n-1��}{2}$ | D�� | $\frac{1}{2}$n��n+1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com