
 下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:
下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
分析 (1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来即可;
(2)计算平均数和回归方程的系数,写出线性回归方程;
(3)利用线性回归方程计算x=100时$\stackrel{∧}{y}$的值,再求出比技改前降低了多少.
解答 解:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图如下: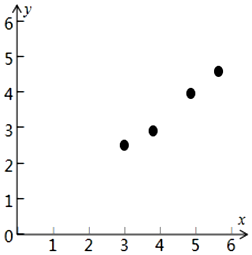
(2)计算$\overline x=\frac{1}{4}(3+4+5+6)=4.5$,
$\overline y=\frac{1}{4}(2.5+3+4+4.5)=3.5$,
$\sum_{i=1}^4{x_1^2={3^2}+{4^2}+{5^2}+{6^2}}=86$,
$\sum_{i=1}^4{{x_i}{y_i}=3×2.5+4×3+5×4+6×4.5}=66.5$,
∴回归方程的系数为
$\hat b=\frac{{\sum_{i=1}^4{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^4{x_1^2-n{{\overline x}^2}}}}=\frac{66.5-4×4.5×3.5}{{86-4×{{4.5}^2}}}=0.7$,
$\hat a=\overline y-\hat b\overline x=3.5-0.7×4.5=0.35$,
所求线性回归方程为$\hat y=0.7x+0.35$;
(3)利用线性回归方程计算x=100时,
$\hat y=0.7×100+0.35=70.35$,
又90-70.35=19.65,
即比技改前降低了19.65吨.
点评 本题考查了散点图与线性回归方程的应用问题,是基础题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或$\frac{1}{2}$ | B. | 3或$\frac{1}{3}$ | C. | 1 | D. | 4或$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n | B. | n-1 | C. | $\frac{n(n-1)}{2}$ | D. | $\frac{1}{2}$n(n+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com