
| A. | 2或$\frac{1}{2}$ | B. | 3或$\frac{1}{3}$ | C. | 1 | D. | 4或$\frac{1}{4}$ |
分析 设抛物线方程,代入椭圆方程,设$\overrightarrow{AF}$=λ$\overrightarrow{FB}$,根据向量数量积的坐标运算,即可求得λ的值,分类讨论,根据抛物线的定义及相似性,即可求得丨BD丨及丨AD丨,即可求得$\frac{|AD|}{|BD|}$的值.
解答 解:抛物线C:y2=2px(p>0)的焦点F($\frac{p}{2}$,0),过A和B分别做准线的垂线,垂足分别为A′,B′,
则直线AB的方程:y=$\frac{4}{3}$(x-$\frac{p}{2}$)设A(x1,y1),B(x2,y2),
$\left\{\begin{array}{l}{y=\frac{4}{3}(x-\frac{p}{2})}\\{{y}^{2}=2px}\end{array}\right.$,整理得:y2-$\frac{3}{2}$py-p2=0,
则y1+y2=$\frac{3}{2}$p,y1y2=-p2,
设$\overrightarrow{AF}$=λ$\overrightarrow{FB}$,($\frac{p}{2}$-x1,-y1)=(x2-$\frac{p}{2}$,y2),则-y1=λy2,由$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$+$\frac{{y}_{2}}{{y}_{1}}$+2=-$\frac{9}{4}$,
∴-λ-$\frac{1}{λ}$+2=-$\frac{9}{4}$,整理得:λ2-17λ+4=0,解得:λ=4或λ=$\frac{1}{4}$,
当λ=4时,丨AF丨=4丨BF丨,则丨AB丨=5丨BF丨,
由抛物线的定义可知:丨BF丨=丨BB′丨,
由直线AB的斜率为$\frac{4}{3}$,则sin∠∠BDB′=$\frac{3}{5}$,即sin∠BDB′=$\frac{丨BB′丨}{丨BD丨}$=$\frac{4}{3}$,
∴丨BD丨=$\frac{5}{3}$丨BB′丨=$\frac{5}{3}$丨BF丨,丨AD丨=丨AB丨+丨BD丨=$\frac{20}{3}$,
∴$\frac{|AD|}{|BD|}$的值4,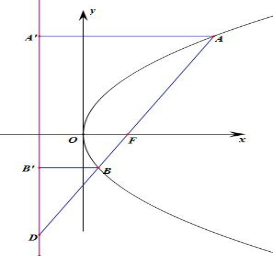
当λ=$\frac{1}{4}$,4丨AF丨=丨BF丨,则丨AB丨=5丨AF丨,
由抛物线的定义可知:丨AF丨=丨AB′丨,
由直线AB的斜率为$\frac{4}{3}$,则sin∠∠ADF′=$\frac{3}{5}$,即sin∠ADF′=$\frac{丨AA′丨}{丨AD丨}$=$\frac{4}{3}$,
∴丨AD丨=$\frac{5}{3}$丨AB′丨=$\frac{5}{3}$丨AF丨,丨BD丨=丨AB丨+丨AD丨=$\frac{20}{3}$,
∴$\frac{|AD|}{|BD|}$的值$\frac{1}{4}$,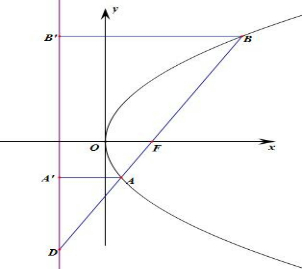
故选D.
点评 本题考查直线与抛物线的位置关系,考查韦达定理,向量的坐标运算,考查数形结合思想,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
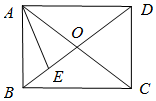 在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.
在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{ln3}{3}$,-$\frac{ln2}{2}$] | B. | (-$\frac{1}{e}$,-$\frac{ln2}{2}$] | C. | [$\frac{ln2}{2}$,-$\frac{ln3}{3}$] | D. | [$\frac{ln2}{2}$,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
| 购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
| A. | 1.79万元 | B. | 2.55万元 | C. | 1.91万元 | D. | 1.94万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:
下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com