
分析 (Ⅰ)直线l的参数方程消去参数t,能求出直线l的普通方程,由ρ2=x2+y2,y=ρsinθ,能求出曲线C的直角坐标方程.
(Ⅱ)设直线l被曲线C截得的弦为AB,A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{2x-y-1=0}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,求出A、B的坐标,由此能求出|AB|.
解答 解:(Ⅰ)∵直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=1+2t}\end{array}\right.$(t为参数),
∴消去参数t,得直线l的普通方程为2x-y-1=0.
∵曲线C的极坐标方程是ρ2=$\frac{4}{1+3si{n}^{2}θ}$,
∴由ρ2=x2+y2,y=ρsinθ,得曲线C的直角坐标方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(Ⅱ)设直线l被曲线C截得的弦为AB,A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{2x-y-1=0}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{16}{17}}\\{y=\frac{15}{17}}\end{array}\right.$,
∴|AB|=$\sqrt{(\frac{16}{17}+0)^{2}+(\frac{15}{17}+1)^{2}}$=$\frac{16\sqrt{5}}{17}$.
点评 本题考查直线的普通方程和曲线的直角坐标方程的求法,考查线段长的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:填空题
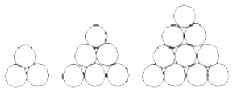 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
| 购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
| A. | 1.79万元 | B. | 2.55万元 | C. | 1.91万元 | D. | 1.94万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 4 | 5 |
| 5 | 2 |
| 6 | 4 5 6 8 |
| 7 | 0 5 5 8 8 8 8 9 |
| 8 | 0 0 5 5 |
| 9 | 4 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:
下表提供了某公司技术升级后生产A产品过程中记录的产量x(吨)与相应的成本y(万元)的几组对照数据:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,EF=$\frac{1}{2}$AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证:
如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,EF=$\frac{1}{2}$AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±3x | B. | $y=±\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{3}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a≤-$\frac{3}{4}$ | C. | a≥1或a<-$\frac{3}{4}$ | D. | a>1或a≤-$\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com