
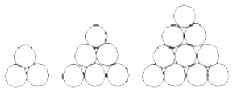
 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示). 分析 观察图形,结合已知可得f(1)=1,f(2)=4,f(3)=10,由图中的规律可得f(n)-f(n-1)=(1+2+3+…+n)从而可得f(n)=f(1)+[f(2)-f(1)]+[f(3)-f(2)]+…+[f(n)-f(n-1)]代入可求.
解答 解:由题意知,f(1)=1,f(2)=1+1+2,f(3)=1+1+2+1+2+3=10,…,
f(n)=1+1+2+1+2+3+…+1+2+3+…+n,
分析可得:f(n)-f(n-1)=1+2+3+…+n=$\frac{n(n+1)}{2}$=$\frac{{n}^{2}}{2}$+$\frac{n}{2}$;
f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n-2)]+[f(n-2)-f(n-3)]+…+f(2)-f(1)+f(1)
=$\frac{1}{2}$(12+22+32+…+n2)=$\frac{1}{12}$n(n+1)(2n+1)+$\frac{1}{4}$n(n+1)=$\frac{1}{6}$n(n+1)(n+2).
故答案为:10,$\frac{1}{6}$n(n+1)(n+2).
点评 本题主要考查数列求和在实际中的应用,解决问题的关键是先由f(1)、f(2)、f(3)的值通过归纳推理得到f(n)的表达式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com